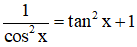Chứng minh các bất đẳng thức sau trang 10 sgk Giải tích 12
Toán lớp 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
Bài 5 (trang 10 SGK Giải tích 12): Chứng minh các bất đẳng thức sau:
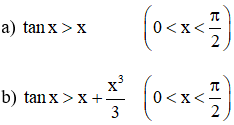
Lời giải:
a) Xét hàm số y = f(x) = tanx – x trên khoảng (0; π/2)
Ta có: y’ =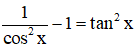 
> 0 với ∀ x ∈ R.
⇒ hàm số đồng biến trên khoảng (0; π/2)
⇒ f(x) > f(0) = 0 với ∀ x > 0
hay tan x – x > 0 với ∀ x ∈ (0; π/2)
⇔ tan x > x với ∀ x ∈ (0; π/2) (đpcm).
b) Xét hàm số y = g(x) = tanx - x -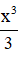 
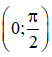
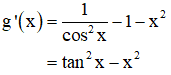
trên 
Theo kết quả câu a): tanx > x ∀ x ∈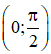 
⇒ g'(x) > 0 ∀ x ∈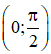
⇒ y = g'(x) đồng biến trên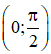
⇒ g(x) > g(0) = 0 với ∀ x ∈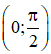
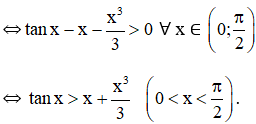
Kiến thức áp dụng
+ Hàm số y = f(x) có đạo hàm trên khoảng K xác định:
Nếu f’(x) < 0 với mọi x ∈ K thì hàm số f(x) nghịch biến trên K.
Nếu f’(x) > 0 với mọi x ∈ K thì hàm số f(x) đồng biến trên K.
+ 
