Giáo án Toán 12 Bài 4: Đường tiệm cận

---

Giáo án Toán 12 Bài 4: Đường tiệm cận

Xem thử

Chỉ 250k mua trọn bộ Giáo án Toán 12 bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0712000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

I. Mục tiêu

1. Kiến thức

- Nắm khái niệm đường tiệm cận đứng, đường tiệm cận ngang của đồ thị hàm số.

2. Năng lực

- Năng lực tự học: Học sinh xác định đúng đắn động cơ thái độ học tập; tự đánh giá và điều chỉnh được kế hoạch học tập; tự nhận ra được sai sót và cách khắc phục sai sót.

- Năng lực giải quyết vấn đề: Biết xác định được đường tiệm cận đứng, đường tiệm cận ngang và phương trình của chúng từ đồ thị hàm số $y=\frac{ax+b}{cx+d}$.

- Năng lực tự quản lý: Làm chủ cảm xúc của bản thân trong quá trình học tập vào trong cuộc sống; trưởng nhóm biết quản lý nhóm mình, phân công nhiệm vụ cụ thể cho từng thành viên nhóm, các thành viên tự ý thức được nhiệm vụ của mình và hoàn thành được nhiệm vụ được giao.

- Năng lực giao tiếp: Tiếp thu kiến thức trao đổi học hỏi bạn bè thông qua hoạt động nhóm; có thái độ tôn trọng, lắng nghe, có phản ứng tích cực trong giao tiếp.

- Năng lực hợp tác: Xác định nhiệm vụ của nhóm, trách nhiệm của bản thân đưa ra ý kiến đóng góp hoàn thành nhiệm vụ của chủ đề.

- Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ Toán học.

3. Phẩm chất

- Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.

- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần trách nhiệmhợp tác xây dựng cao.

- Biết nhận xét và đánh giá bài làm của bạn, cũng như tự đánh giá kết quả học tập của bản thân.

- Chăm chỉ tích cực xây dựng bài, chủ động ghi nhớ lại và vận dụng kiến thức theo sự hướng dẫn của GV.

- Hình thành tư duy logic, lập luận chặt chẽ và linh hoạt trong quá trình suy nghĩ.

II. Thiết bị dạy học và học liệu

- Máy chiếu

- Bảng phụ

- Phiếu học tập

III. Tiến trình dạy học

1. Hoạt động 1: Mở đầu

a) Mục tiêu: Nắm vững các phương pháp tìm giới hạn một bên, giới hạn hữu hạn tại vô cực của hàm số và nhận biết được kết quả giới hạn từ đồ thị hàm số.

b) Nội dung: GV hướng dẫn, tổ chức học sinh ôn tập một số dạng toán xác định giới hạn hàm số.

H1- Tính các giới hạn một bên: $\underset{x\to 2^{-}}{\lim }\frac{x+1}{x-2};\underset{x\to 2^{+}}{\lim }\frac{x+1}{x-2}.$

H2- Tính các giới hạn một bên: $\underset{x\to -\infty }{\lim }\frac{x+1}{x-2};\underset{x\to +\infty }{\lim }\frac{x+1}{x-2}.$

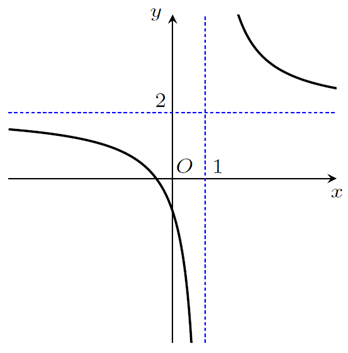
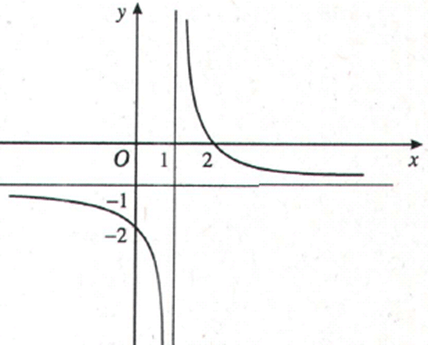
H3- Cho hàm số y - f(x) liên tục và xác định trên R\{1} có đồ thị như hình vẽ dưới đây.

Hãy đánh dấu X vào ô tương ứng với câu trả lời đúng.

...	$\underset{x\to -\infty }{\lim }f\left(x\right)=2$	...........	...	$\underset{x\to 2^{+}}{\lim }f\left(x\right)=+\infty$
...	$\underset{x\to -\infty }{\lim }f\left(x\right)=+\infty$	...........	...	$\underset{x\to 1^{+}}{\lim }f\left(x\right)=+\infty$
...	$\underset{x\to +\infty }{\lim }f\left(x\right)=+\infty$	...........	...	$\underset{x\to 1^{-}}{\lim }f\left(x\right)=-\infty$
...	$\underset{x\to +\infty }{\lim }f\left(x\right)=2$	...........	...	$\underset{x\to 2^{-}}{\lim }f\left(x\right)=-\infty$

c) Sản phẩm:

Câu trả lời của HS

L1- $\underset{x\to 2^{-}}{\lim }\frac{x+1}{x-2}=-\infty ;\underset{x\to 2^{+}}{\lim }\frac{x+1}{x-2}=+\infty .$

L2- $\underset{x\to -\infty }{\lim }\frac{x+1}{x-2}=1;\underset{x\to +\infty }{\lim }\frac{x+1}{x-2}=1.$

L3-

X	$\underset{x\to -\infty }{\lim }f\left(x\right)=2$	.......	$\underset{x\to 2^{+}}{\lim }f\left(x\right)=+\infty$
$\underset{x\to -\infty }{\lim }f\left(x\right)=+\infty$	.......	X	$\underset{x\to 1^{+}}{\lim }f\left(x\right)=+\infty$
$\underset{x\to +\infty }{\lim }f\left(x\right)=+\infty$	.......	X	$\underset{x\to 1^{-}}{\lim }f\left(x\right)=-\infty$
X	$\underset{x\to +\infty }{\lim }f\left(x\right)=2$	.......	$\underset{x\to 2^{-}}{\lim }f\left(x\right)=-\infty$

d) Tổ chức thực hiện:

*) Chuyển giao nhiệm vụ: GV nêu câu hỏi

*)Thực hiện: HS suy nghĩ độc lập

*) Báo cáo, thảo luận:

- GV gọi lần lượt 3 học sinh, lên bảng trình bày câu trả lời của mình.

- Các học sinh khác nhận xét, bổ sung để hoàn thiện câu trả lời.

*) Đánh giá, nhận xét, tổng hợp:

- GV đánh giá thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tổng hợp kết quả.

- Dẫn dắt vào bài mới.

2. Hoạt động 2: Hình thành kiến thức mới

I. Đường tiệm cận ngang

a) Mục tiêu: Hình thành khái niệmđường tiệm cận ngang và biết áp dụng tìm đường tiệm cận ngang

b) Nội dung: GV yêu cầu HS giải bài toán rút ra định nghĩa, đọc SGK và áp dụng làm ví dụ.

H1: Bài toán. Cho hàm số $y=\frac{2-x}{x-1}$có đồ thị (C).

Nhận xét khoảng cách từ điểm M(x;y)$\in$(C) đến đường thẳng $\Delta$: y = -1 khi $x\to \pm \infty$?

H2: Định nghĩa

H3: Chú ý

H4. Cách tìm tiệm cận ngang

H5.Ví dụ 1. Tìm tiệm cận ngang của đồ thị hàm số:

a) $y=\frac{2x-1}{x+1}$

b) $y=\frac{x-1}{x^2+1}$

c) $y=\frac{x^2-3x+2}{x^2+x+1}$

d) $y=\frac{1}{x+7}$

c) Sản phẩm:

I. ĐƯỜNG TIỆM CẬN NGANG 1. Định nghĩa Cho hàm số y=f(x)xác định trên một khoảng vô hạn. Đường thẳng y=y0 là tiệm cận ngang của đồ thị hàm số y=f(x) nếu ít nhất một trong các điều kiện sau được thoả mãn: $\underset{x\to +\infty }{\lim }f\left(x\right)=y_0$, $\underset{x\to -\infty }{\lim }f\left(x\right)=y_0$ Chú ý: Nếu $\underset{x\to +\infty }{\lim }f\left(x\right)=\underset{x\to -\infty }{\lim }f\left(x\right)=y_0$ thì ta viết chung $\underset{x\to \pm \infty }{\lim }f\left(x\right)=y_0$ $\Rightarrow$Cách tìm tiệm cận ngang Nếu tính được $\underset{x\to +\infty }{\lim }f\left(x\right)=y_0$ hoặc $\underset{x\to -\infty }{\lim }f\left(x\right)=y_0$ thì đường thẳng y=y0 là TCN của đồ thị hàm số y=f(x) 2. Ví dụ 1: Tìm tiệm cận ngang của đồ thị hàm số: a) $y=\frac{2x-1}{x+1}$ b) $y=\frac{x-1}{x^2+1}$ c) y = $\frac{x^2-3x+2}{x^2+x+1}$ d) y = $\frac{1}{x+7}$ ĐS : a) TCN: y = 2 b) TCN: y = 0 c) TCN: y = 1 d) TCN: y = 0

d) Tổ chức thực hiện

Chuyển giao	- GV dẫn dắt từ bài toán để hình thành khái niệm đường tiệm cận ngang. - HS thực hiện bài toán rồi rút ra định nghĩa đường tiệm cận ngang + Tính khoảng cách từ M đến $∆$ ? d(M;$∆$) = |y+1| + Nhận xét khoảng cách đó khi x$\to \pm \infty$ ? dần tới 0 + Hình thành định nghĩa đường tiệm cận ngang
Thực hiện	- HS thảo luận theo nhóm thực hiện nhiệm vụ - GV theo dõi, hỗ trợ , hướng dẫn các nhóm
Báo cáo thảo luận	- HS nêu được định nghĩa tiệm cận ngang và thực hiện VD1. - GV gọi 4 HS lên bảng trình bày lời giải cho VD1 - HS khác theo dõi, nhận xét, hoàn thiện sản phẩm
Đánh giá, nhận xét, tổng hợp	- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức: Nếu tính được $\underset{x\to +\infty }{lim}f\left(x\right)=y_0$ hoặc $\underset{x\to -\infty }{lim}f\left(x\right)=y_0$ thì đường thẳng y=y0 là TCN của đồ thị hàm số y=f(x).

................................

................................

................................

Trên đây tóm tắt một số nội dung có trong bộ Giáo án Toán 12 năm 2023 mới nhất, để mua tài liệu đầy đủ, Thầy/Cô vui lòng truy cập Tài liệu Giáo án, đề thi mới, chuẩn

Xem thử