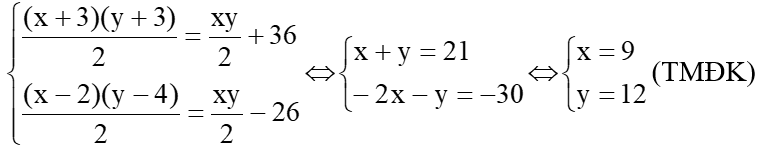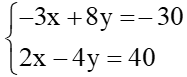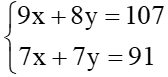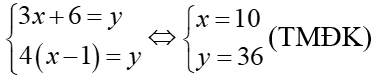Giáo án Toán 9 Luyện tập trang 24-25 mới nhất
Giáo án Toán 9 Luyện tập trang 24-25 mới nhất
I. Mục tiêu:
Qua bài này giúp HS:
1. Kiến thức
- HS phân tích và lập luận được để giải một số bài toán năng suất, toán chuyển động bằng cách lập hệ phương trình.
- Trình bày được lời giải bài toán một cách logic.
2. Kỹ năng
- Vận dụng được kiến thức vào thực tế, liên hệ để thấy được ứng dụng của Toán học trong đời sống.
3. Thái độ
- Nghiêm túc và hứng thú học tập.
- Yêu thích môn học.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán
- Năng lực giải quyết vấn đề
- Năng lực hợp tác.
- Năng lực ngôn ngữ
- Năng lực giao tiếp.
- Năng lực tự học.
Phẩm chất: Tự tin, tự chủ
II. Chuẩn bị
- Giáo viên:bảng phụ, thước thẳng, phấn màu, máy tính bỏ túi
- Học sinh: máy tính bỏ túi, thước thẳng.
III. Tiến trình bài dạy
1. Ổn định tổ chức
2. Nội dung:
| Giáo viên | Học sinh | Nội dung ghi bài |
|---|---|---|
|
Hoạt động 1: Khởi động – 8p GV gọi 1 học lên bảng chữa bài 31/sgk. Đáp án: Gọi hai cạnh của tam giác vuông ban đầu là x và y (x, y > 0) Theo đề bài ta có hệ phương trình:
Vậy độ dài hai cạnh góc vuông của tam giác vuông là 9 cm và 12 cm. |
||
|
Hoạt động 2: Luyện tập -32p - Mục tiêu: HS nêu được các đại lượng trong bài, nêu được ẩn phụ cần đặt cho bài toán, thiết lập và giải được hệ phương trình đã lập. - Phương pháp: Nêu vấn đề, thuyết trình, vấn đáp. |
||
Cho học sinh đọc yêu cầu của đề bài ? Bài toán có những đại lượng nào. ? Để biết số cây trong vườn cần biết đại lượng nào ? Hãy chọn ẩn và đặt điều kiện cho ẩn ? Khi đó số cây trong vườn là bao nhiêu? Nếu tăng thêm 8 luống nhưng mỗi luống giảm 3 cây, và số cây khi đó giảm đi 54 thì ta có điều gì Nếu giảm đi 4 luống nhưng mỗi luống tăng thêm 2 cây và số cây khi đó tăng thêm 32 cây thì ta có điều gì? Từ đó ta có hệ phương trình nào? Hãy giải hệ phương trình trên? GV đưa bảng phụ ghi đề bài lên bảng Gọi HS đọc yêu cầu của bài toán (HS hoạt động nhóm sau đó mời đại diện nhóm lên bảng trình bày) GV đưa bài tập lên bảng phụ: “Trong phòng học có 1 số ghế dài, nếu xếp mỗi ghế 3 HS thì 6 HS không có chỗ. Nếu xếp mỗi ghế 4 HS thì thừa 1 ghế. Hỏi cả lớp có bao nhiêu ghế? ” (HS hoạt động nhóm sau đó mời đại diện nhóm lên bảng trình bày) |
(HS hoạt động cá nhân/ cặp đôi) HS đọc yêu cầu của đề bài Và tóm tắt bài toán HS: Số luống cây trong một luống, sô cây trong vườn Khi đó số cây trong vườn là xy Khi đó ta có (x + 8)(y - 3) = xy - 54 Khi đó ta có (x - 4)(y + 2) = xy + 32 Ta Có:
HS giải hệ phương trình trên và trả lời bài toán HS đọc đề Và tóm tắt bài toán HS thảo luận làm bài, 1 HS lên bảng trình bày HS đọc yêu cầu của bài toán HS thảo luận làm bàivào bảng phụ nhóm Các nhóm báo cáo kết quả HS giải hệ phương trình trên và trả lời câu hỏi của đề bài |
Bài 34/24-SGK: Giải : Gọi x là số luống trong vườn, y là số cây trong mỗi luống. ĐK: x; y ≥ 0 Khi đó số cây trong vườn là xy (cây) Theo bài ra ta có: (x + 8)(y - 3) = xy - 54 <=> -3x + 8y = -30 (1) Và (x - 4)(y + 2) = xy + 32 <=> 2x - 4y = 40 (2) Từ (1) và (2) ta có hệ phương trình:
Giải hệ phương trình trên ta có: x = 50 Và y = 15 (TMĐK) Vậy vườn nhà Lan trồng 50.15 = 750 Cây cải bắp. Bài 35/24-SGK: Giải: Gọi x (rupi) và y (rupi) lần lượt là giá của mỗi quả thanh yên và táo rừng thơm. ĐK: x; y > 0 Theo bài ra ta có hệ phương trình:
Giải hệ phương trình trên ta có x = 3 và y = 10(TMĐK) Vậy giá mỗi quả thanh yên là 3 rupi, của quả táo rừng thơm là 10 rupi. Bài tập: Giải: Gọi x là số ghế Số học sinh của lớp là y ĐK: x, y ∈ N* Theo bài ra ta có hệ :
Vậy lớp có 10 ghế; 36 học sinh |
|
Hoạt động 3: Tìm tòi, mở rộng – 5p - Mục tiêu: - HS chủ động làm các bài tập về nhà để củng cố kiến thức đã học. - HS chuẩn bị bài mới giúp tiếp thu tri thức sẽ học trong buổi sau. - Kĩ thuật sử dụng: Kĩ thuật viết tích cực, trình bày 1 phút |
||
GV củng cố lại kiến thức đã học trong bài + Bài tập về nhà: 37, 38, 39/24 ,25 SGK. 43, 44, 45/10 SBT. Chuẩn bị tiết sau luyện tập. |
||
|
- Hướng dẫn bài 37 – SGK Gọi vận tốc của vật chuyển động nhanh là x (cm/s) Và vận tốc của vật chuyển động chậm là y (cm/s) (x, y > 0) Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường mà vật đi nhanh đi được trong 20 giây hơn quãng đường vật đi chậm cũng trong 20 giây đúng 1 vòng. Ta có phương trình 20x - 20y = 20π Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, ta có phương trình 4x + 4y = 20π Từ đó có HPT và giải HPT. |
||