Cho tam giác ABC, biết tọa độ trung điểm các cạnh BC, CA, AB
Cho tam giác ABC, biết tọa độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1; 1), N(3; 4), P(5; 6).
Giải sách bài tập Toán 10 Bài 3: Phương trình đường thẳng
Bài 29 trang 73 SBT Toán 10 Tập 2: Cho tam giác ABC, biết tọa độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1; 1), N(3; 4), P(5; 6).
a) Viết phương trình tham số của các đường thẳng AB, BC, CA.
b) Viết phương trình tổng quát của các đường trung trực của tam giác ABC.
Lời giải:
a) Xét tam giác ABC có: M, N là trung điểm của BC, AC.
Do đó MN là đường trung bình của tam giác ABC.
Suy ra MN song song với AB.
Tương tự ta có MP song song với AC, NP song song với BC.
MN song song với AB nên =(4;3) là vectơ chỉ phương của AB
Mà P(5; 6) thuộc AB nên phương trình tham số của AB là: 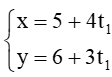
Ta có: =(2;2)=2(1;1) là vectơ chỉ phương của BC và điểm M(– 1; 1) thuộc AB nên phương trình tham số của BC: 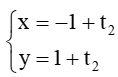
Ta có: =(6;5) là vectơ chỉ phương của AC và điểm N(3; 4) thuộc AB nên phương trình tham số của AC: 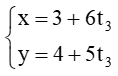
b) Gọi d1,d2,d3 là đường trung trực của AB, BC, AC.
Do MN song song với AB nên = (4; 3) là vectơ pháp tuyến của d1. Đường thẳng d1 đi qua P(5; 6) nên d1 có phương trình tổng quát là:
4(x – 5) + 3(y – 6) = 0 hay 4x + 3y – 38 = 0.
Do NP song song với BC nên =(2;2)=2(1;1) là vectơ pháp tuyến của d2. Đường thẳng d2 đi qua M(– 1; 1) nên d2 có phương trình tổng quát là:
1(x + 1) + 1(y – 1) = 0 hay x + y = 0.
Do NP song song với BC nên =(6;5) là vectơ pháp tuyến của d2. Đường thẳng d2 đi qua N(3; 4) nên d2 có phương trình tổng quát là:
6(x – 3) + 5(y – 4) = 0 hay 6x + 5y – 38 = 0.

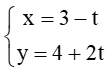 . Vectơ nào dưới đây là một vectơ chỉ phương của ∆? ....
. Vectơ nào dưới đây là một vectơ chỉ phương của ∆? ....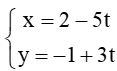 . Trong các điểm có tọa độ dưới đây, điểm nào nằm trên đường thẳng ∆? ....
. Trong các điểm có tọa độ dưới đây, điểm nào nằm trên đường thẳng ∆? ....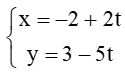 . Phương trình nào dưới đây là phương trình tổng quát của ∆? ....
. Phương trình nào dưới đây là phương trình tổng quát của ∆? ....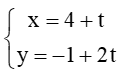 và điểm A(2; 1). Hai điểm M, N nằm trên ∆ ....
và điểm A(2; 1). Hai điểm M, N nằm trên ∆ ....