Cho ba điểm A(- 2; 2), B(7; 5), C(4; - 5) và đường thẳng ∆: 2x + y – 4 = 0
Cho ba điểm A(- 2; 2), B(7; 5), C(4; - 5) và đường thẳng ∆: 2x + y – 4 = 0.
Giải sách bài tập Toán 10 Bài 3: Phương trình đường thẳng
Bài 32 trang 74 SBT Toán 10 Tập 2: Cho ba điểm A(- 2; 2), B(7; 5), C(4; - 5) và đường thẳng ∆: 2x + y – 4 = 0.
a) Tìm tọa độ điểm M thuộc ∆ và cách đều hai điểm A và B.
b*) Tìm tọa độ điểm N thuộc ∆ sao cho || có giá trị nhỏ nhất.
Lời giải:
a) Do M thuộc đường thẳng ∆ nên M(t; 4 – 2t).
Suy ra =(t+2;2-2t) và =(t-7;-1-2t).
Do M cách đều 2 điểm A, B nên MA = MB.
Hay ||= ||
⇔ 5t2 – 4t + 8 = 5t2 – 10t + 50
⇔ 6t = 42
⇔ t = 7
Vậy M(7; -10).
b) Do N thuộc đường thẳng ∆ nên N(m; 4 – 2m).
Suy ra =(-2-2;2m-2), =(7-m;2m+1) và =(4-1;2m-9)
= (9-3m;6m-10)
Gọi A= (9-3m)2+(6m-10)2
A=45m2 - 174m+181=45
Suy ra GTNN của || là đạt được khi m=
Hay .

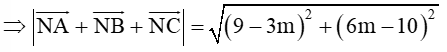
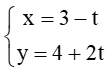 . Vectơ nào dưới đây là một vectơ chỉ phương của ∆? ....
. Vectơ nào dưới đây là một vectơ chỉ phương của ∆? ....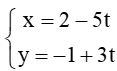 . Trong các điểm có tọa độ dưới đây, điểm nào nằm trên đường thẳng ∆? ....
. Trong các điểm có tọa độ dưới đây, điểm nào nằm trên đường thẳng ∆? ....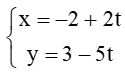 . Phương trình nào dưới đây là phương trình tổng quát của ∆? ....
. Phương trình nào dưới đây là phương trình tổng quát của ∆? ....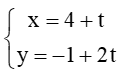 và điểm A(2; 1). Hai điểm M, N nằm trên ∆ ....
và điểm A(2; 1). Hai điểm M, N nằm trên ∆ ....