Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây)

Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,3) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8m sau 1 giây và đạt độ cao 6m sau 2 giây. Trong khoảng thời gian nào (tính bằng giây) thì quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m (làm tròn kết quả đến hàng phần nghìn).

Giải sách bài tập Toán 10 Bài 4: Bất phương trình bậc hai một ẩn

Bài 34 trang 57 SBT Toán 10 Tập 1: Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,3) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8m sau 1 giây và đạt độ cao 6m sau 2 giây. Trong khoảng thời gian nào (tính bằng giây) thì quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m (làm tròn kết quả đến hàng phần nghìn).

Lời giải:

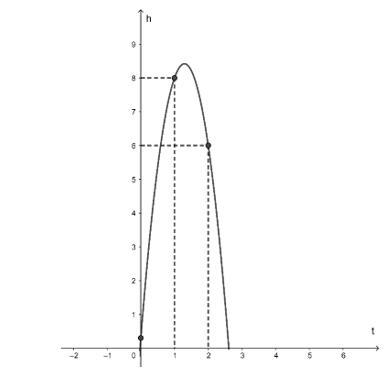
Ta có hình vẽ mô phỏng quỹ đạo chuyển động của quả bóng như hình vẽ:

Vì quỹ đạo chuyển động là một đường thẳng parabol có dạng h = at² + bt + c (a ≠ 0).

Một quả bóng được đá lên từ điểm A(0; 0,3) nên điểm A thuộc vào parabol, thay t = 0 và h = 0,3 vào đồ thị hàm số ta được: 0,3 = a.0² + b.0 + c ⇔ c = 0,3 (1).

Bóng đạt độ cao h = 8m sau t = 1 giây nên điểm có tọa độ (1; 8) thuộc vào parabol.

Thay t = 1 và h = 8 vào đồ thị hàm số ta được: 8 = a.1² + b.1 + c ⇔ a + b + c = 8 (2).

Bóng đạt độ cao h = 6m sau t = 2 giây nên điểm có tọa độ (2; 6) thuộc vào parabol.

Thay t = 2 và h = 6 vào đồ thị hàm số ta được: 6 = a.2² + b.2 + c ⇔ 4a + 2b + c = 6 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}c = 0,3\\ a + b + c = 8\\ 4a + 2b + c = 6\end{array}\right.\iff \left\{\begin{array}{l}c = 0,3\\ a = -4,85\\ b = 12,55\end{array}\right.$.

Ta có phương trình parabol cần tìm là: h = – 4,85t² + 12,55t + 0,3.

Để chiều cao lớn hơn 5 thì h > 5 ⇔ – 4,85t² + 12,55t + 0,3 > 5

⇔ – 4,85t² + 12,55t – 4,7 > 0

Xét tam thức bậc hai f(t) = – 4,85t² + 12,55t – 4,7, có a = – 4,85, ∆ = 12,55² – 4.(– 4,85).(– 4,7) = 66,3225 > 0.

Suy ra tam thức có hai nghiệm phân biệt t₁ ≈ 0,454 và t₂ ≈ 2,133.

Áp dụng định lí về dấu của tam thức bậc hai ta được: f(t) > 0 hay – 4,85t² + 12,55t – 4,7 > 0 khi t ∈ (0,454; 2,133).

Để chiều cao nhỏ hơn 7 thì h < 7 ⇔ – 4,85t² + 12,55t + 0,3 < 7

⇔ – 4,85t² + 12,55t – 6,7 < 0

Xét tam thức bậc hai g(t) = – 4,85t² + 12,55t – 6,7, có a = – 4,85, ∆ = 12,55² – 4.(– 4,85).(– 6,7) = 27,5225 > 0.

Suy ra tam thức có hai nghiệm phân biệt t₁ ≈ 0,753 và t₂ ≈ 1,835.

Áp dụng định lí về dấu của tam thức bậc hai ta được: g(t) < 0 hay – 4,85t² + 12,55t – 6,7 < 0 khi t ∈ (– ∞; 0,753) ∪ (1,835; +∞).

Để quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m thì t phải thuộc vào giao của hai tập (0,454; 2,133) hoặc (– ∞; 0,753) ∪ (1,835; +∞).

Ta có (0,454; 2,133)  (– ∞; 0,753) ∪ (1,835; +∞) = (0,454; 0,753) ∪ (1,835; 2,133).

Vậy để quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m thì thuộc khoảng 0,454 giây đến 0,753 giây hoặc 1,835 giây đến 2,133 giây.