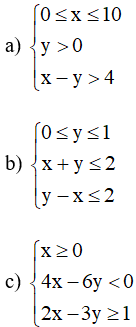Biểu diễn miền nghiệm của các hệ bất phương trình bậc nhất hai ẩn Bài 2.26 trang 27 sách bài tập Toán 10 tập 1
Giải sách bài tập Toán lớp 10 Bài tập cuối chương II
Bài 2.26 trang 27 sách bài tập Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
Lời giải:
a) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1)∉ d1 và thay vào biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Đường thẳng d2: x = 10 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 10.
Chọn điểm I(1; 1) ∉ d2 và thay vào biểu thức x ta được 1 < 10.
Suy ra miền nghiệm của bất phương trình x ≤ 10 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1).
• Đường thẳng d3: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(1; 1) ∉ d3 và thay vào biểu thức y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình y > 0 là nửa mặt phẳng bờ d3 chứa điểm I(1; 1) và bỏ đi đường thẳng d3.
• Vẽ đường thẳng d4: x - y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (4; 0) và (0; -4).
Chọn điểm I(1; 1) ∉ d4 và thay vào biểu thức x - y ta được 0 < 4.
Suy ra miền nghiệm của bất phương trình x - y > 4 là nửa mặt phẳng bờ d4 không chứa điểm I(1; 1) và bỏ đi đường thẳng d4.
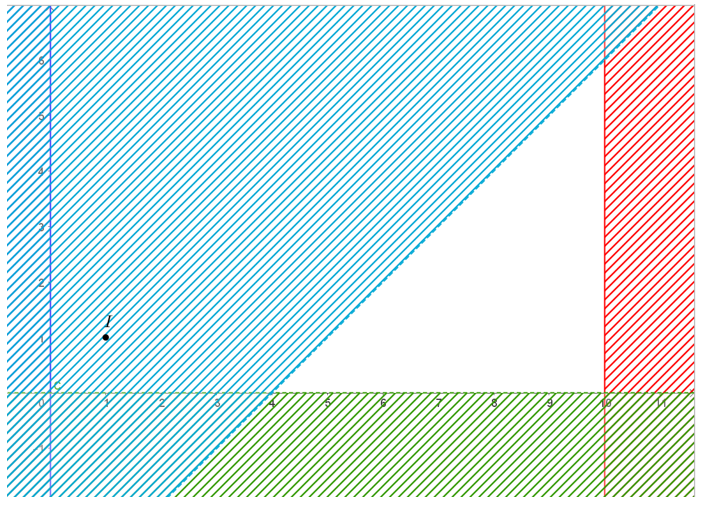
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
b) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(0; 0,5) Ï d1 và thay vào biểu thức y ta được 0,5 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(0; 0,5).
• Đường thẳng d2: y = 1 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 1.
Chọn điểm I(0; 0,5) ∉ d2 và thay vào biểu thức y ta được 0,5 < 1.
Suy ra miền nghiệm của bất phương trình y ≤ 1 là nửa mặt phẳng bờ d2 chứa điểm I(0; 0,5).
• Vẽ đường thẳng d3: x + y = 2 bằng cách vẽ đường thẳng đi qua hai điểm (2; 0) và (0; 2).
Chọn điểm I(0; 0,5) ∉ d3 và thay vào biểu thức x + y ta được 0,5 < 2.
Suy ra miền nghiệm của bất phương trình x + y ≤ 2 là nửa mặt phẳng bờ d3 chứa điểm I(0; 0,5).
• Vẽ đường thẳng d4: y - x = 2 bằng cách vẽ đường thẳng đi qua hai điểm (0; 2) và (-2; 0).
Chọn điểm I(0; 0,5) ∉ d4 và thay vào biểu thức y - x ta được 0,5 < 2.
Suy ra miền nghiệm của bất phương trình y - x ≤ 2 là nửa mặt phẳng bờ d4 chứa điểm I(0; 0,5).
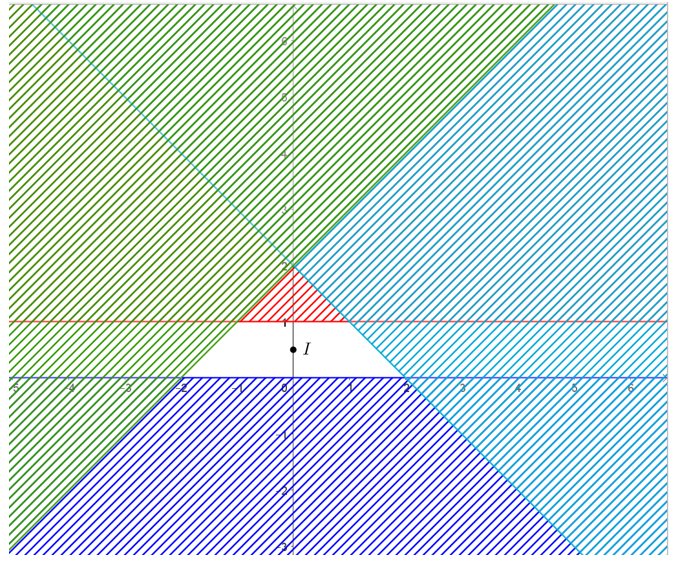
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
c) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Vẽ đường thẳng d2: 4x - 6y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (3; 2).
Chọn điểm I(1; 1)∉d2 và thay vào biểu thức 4x - 6y ta được -2 < 0.
Suy ra miền nghiệm của bất phương trình 4x - 6y < 0 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1) và bỏ đi đường thẳng d2.
• Vẽ đường thẳng d3: 2x - 3y = 1 bằng cách vẽ đường thẳng đi qua hai điểm (2; 1) và (5; 3).
Chọn điểm I(1; 1) ∉ d3 và thay vào biểu thức 2x - 3y ta được -1 < 1.
Suy ra miền nghiệm của bất phương trình 2x - 3y ≥ 1 là nửa mặt phẳng bờ d3 không chứa điểm I(1; 1).
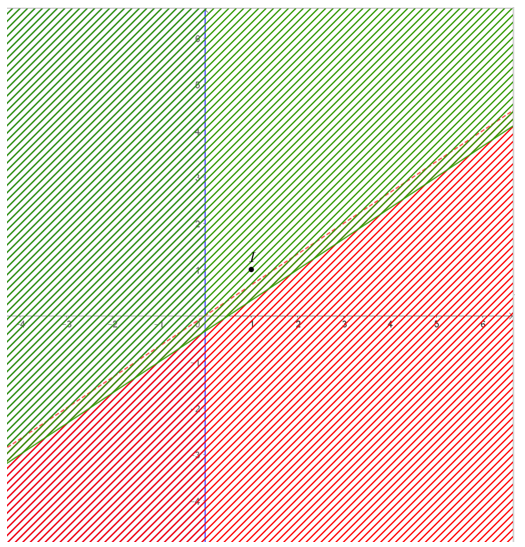
Khi đó hệ vô nghiệm vì mặt phẳng tọa độ đều bị gạch.