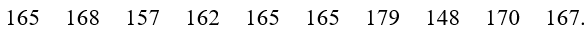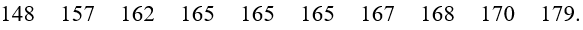Mẫu số liệu sau là chiều cao (đơn vị: cm) của các bạn trong tổ của Lan

Mẫu số liệu sau là chiều cao (đơn vị: cm) của các bạn trong tổ của Lan:

Sách bài tập Toán 10 Kết nối tri thức Bài 14: Các số đặc trưng đo độ phân tán

Bài 5.17 trang 81 sách bài tập Toán lớp 10 Tập 1: Mẫu số liệu sau là chiều cao (đơn vị: cm) của các bạn trong tổ của Lan:

a) Tính khoảng tứ phân vị của mẫu số liệu trên.

b) Khoảng tứ phân vị có bị ảnh hưởng bởi chiều cao của bạn cao nhất, bạn thấp nhất không?

Lời giải:

a) Sắp xếp dãy số liệu theo thứ tự không giảm ta được:

• Vì n = 10 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa (số liệu thứ 5 và thứ 6) của mẫu số liệu đã sắp xếp.

Do đó Q₂ = $\frac{165+165}{2}=165.$

• Nửa dữ liệu bên trái Q₂ là: 148; 157; 162; 165; 165.

Dãy này gồm 5 số liệu, n = 5 là số lẻ nên trung vị là giá trị chính giữa (số liệu thứ 3 của nửa dữ liệu bên trái Q₂) nên Q₁ = 162.

• Nửa dữ liệu bên phải Q₂ là: 165; 167; 168; 170; 179.

Dãy này gồm 5 số liệu, n = 5 là số lẻ nên trung vị là giá trị chính giữa (số liệu thứ 3 của nửa dữ liệu bên phải Q₂) nên Q₃ = 168.

Khi đó khoảng tứ phân vị của mẫu số liệu đã cho là:

$∆$_Q = Q₃ – Q₁ = 168 – 162 = 6.

Vậy khoảng tứ phân vị của mẫu số liệu đã cho là 6 cm.

b) Khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp nên đo độ phân tán của 50% dữ liệu này.

Do đó khoảng tứ phân vị không bị ảnh hưởng bởi giá trị nhỏ nhất, giá trị lớn nhất.

Vậy khoảng tứ phân vị không bị ảnh hưởng bởi chiều cao của bạn cao nhất và bạn thấp nhất.