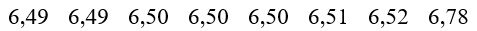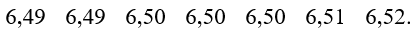Một học sinh dùng một dụng cụ đo đường kính d của một viên bi (đơn vị: mm) thu được kết quả sau

Một học sinh dùng một dụng cụ đo đường kính d của một viên bi (đơn vị: mm) thu được kết quả sau:

Sách bài tập Toán 10 Kết nối tri thức Bài tập cuối chương 5 trang 81, 82, 83, 84

Bài 5.35 trang 84 sách bài tập Toán lớp 10 Tập 1: Một học sinh dùng một dụng cụ đo đường kính d của một viên bi (đơn vị: mm) thu được kết quả sau:

a) Bạn Minh cho rằng kết quả đo ở lần 7 không chính xác. Hãy kiểm tra khẳng định này của Minh.

b) Tìm giá trị xấp xỉ cho đường kính của viên bi.

Lời giải:

a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:

• Vì n = 8 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa (số liệu thứ 4 và 5) của mẫu số liệu đã sắp xếp.

Do đó Q₂ = $\frac{6,50+6,50}{2}=6,50.$

• Nửa dãy số liệu bên trái Q₂ là: 6,49; 6,49; 6,50; 6,50.

Dãy này gồm 4 số, n = 4 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa (số liệu thứ 2 và 3 của dãy số liệu bên trái Q₂).

Do đó Q₁ = $\frac{6,49+6,50}{2}=6,495.$

• Nửa dãy số liệu bên phải Q₂ là: 6,50; 6,51; 6,52; 6,78.

Dãy này gồm 4 số, n = 4 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa (số liệu thứ 2 và 3 của dãy số liệu bên phải Q₂).

Do đó Q₃ = $\frac{6,51+6,52}{2}=6,515.$

Khi đó $∆$_Q = Q₃ – Q₁ = 6,515 – 6,495 = 0,02.

Ta có: Q₁ – 1,5.$∆$_Q = 6,495 – 1,5.0,02 = 6,465;

Và Q₃ + 1,5.$∆$_Q = 6,515 + 1,5.0,02 = 6,545.

Ta thấy 6,78 > 6,545 nên đây là giá trị bất thường.

Do đó kết quả đo ở lần 7 không chính xác.

Vậy khẳng định của Minh là đúng.

b) Vì 6,78 là giá trị bất thường nên ta bỏ giá trị này được mẫu số liệu:

Số trung bình là:

$\overline{x}=\frac{6,49+6,49+6,50+6,50+6,50+6,51+6,52}{7}\approx 6,50$

Vậy giá trị xấp xỉ cho đường kính của viên bi là 6,50 mm.