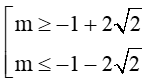Tìm điều kiện của tham số m để phương trình sau có nghiệm

Tìm điều kiện của tham số m để phương trình sau có nghiệm: .

Sách bài tập Toán 10 Kết nối tri thức Bài 18: Phương trình quy về phương trình bậc hai

Bài 6.31 trang 21 Sách bài tập Toán lớp 10 Tập 2: Tìm điều kiện của tham số m để phương trình sau có nghiệm: $\sqrt{2x^2+x+1}=\sqrt{x^2+mx+m-1}$.

Lời giải:

$\sqrt{2x^2+x+1}=\sqrt{x^2+mx+m-1}$ (1)

Bình phương hai vế của (1) ta có:

2x² + x + 1 = x² + mx + m – 1

⇔ x² + (1 – m)x + 2 – m = 0 (2)

Xét tam thức bậc hai f(x) = 2x² + x + 1 có: a = 2 > 0, ∆_f = 1² – 4.2.1 = –7 < 0

Do đó, f(x) = 2x² + x + 1 > 0 với mọi số thực x nên x² + mx + m – 1 > 0 với mọi số thực x, do đó, $\sqrt{2x^2+x+1}$, $\sqrt{x^2+mx+m-1}$ luôn có nghĩa với mọi số thực x.

Do đó, (1) có nghiệm khi và chỉ khi (2) có nghiệm.

Xét phương trình bậc hai (2) ta có:

∆ = (1 – m)² – 4.1.(2 – m) = 1 – 2m + m² – 8 + 4m = m² + 2m – 7

Phương trình (2) có nghiệm khi và chỉ chi ∆ ≥ 0

⇔ m² + 2m – 7 ≥ 0

Xét phương trình bậc hai ẩn m là: m² + 2m – 7 = 0 có:

a = 1 > 0

∆_m = 2² – 4.1.(–7) = 32 > 0

Do đó, phương trình có hai nghiệm phân biệt là: $m_1=-1+2\sqrt{2};m_2=-1-2\sqrt{2}$

Do đó, m² + 2m – 7 ≥ 0 ⟺

Vậy khi $m\ge -1+2\sqrt{2}$ hoặc $m\le -1-2\sqrt{2}$ thì phương trình $\sqrt{2x^2+x+1}=\sqrt{x^2+mx+m-1}$ có nghiệm.