Trong mặt phẳng Oxy, cho điểm M(2; 1) và đường thẳng ∆

Trong mặt phẳng Oxy, cho điểm M(2; 1) và đường thẳng . Tìm điểm N thuộc đường thẳng ∆ sao cho .

Sách bài tập Toán 10 Kết nối tri thức Bài 19: Phương trình đường thẳng

Bài 7.6 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho điểm M(2; 1) và đường thẳng 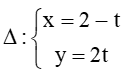. Tìm điểm N thuộc đường thẳng ∆ sao cho $MN=\sqrt{2}$.

Lời giải:

Do N thuộc đường thẳng ∆ nên tọa độ của N có dạng: (2 – t; 2t).

Ta có: $\overrightarrow{MN}$ = (2 – t – 2; 2t – 1) = (–t; 2t – 1)

$MN=\sqrt{2}$

$\iff \sqrt{{(-t)}^2+{(2t-1)}^2}=\sqrt{2}$

⇔ (– t)² + (2t – 1)² = 2

⇔ t² + 4t² – 4t + 1 = 2

⇔ 5t² – 4t – 1 = 0

⇔ t = 1 hoặc t = $-\frac{1}{5}$

Với t = 1, ta có N(1; 2)

Với t = $-\frac{1}{5}$, ta có $N\left(\frac{11}{5};-\frac{2}{5}\right)$.

Vậy có hai điểm N thỏa mãn là N(1; 2) và $N\left(\frac{11}{5};-\frac{2}{5}\right)$.