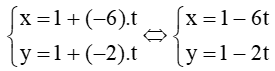Trong mặt phẳng Oxy, cho tam giác ABC có toạ độ ba đỉnh A(0; –1), B(2; 3) và C(–4; 1)

Trong mặt phẳng Oxy, cho tam giác ABC có toạ độ ba đỉnh A(0; –1), B(2; 3) và C(–4; 1). Lập phương trình tham số của đường trung bình ứng với cạnh BC của tam giác ABC.

Sách bài tập Toán 10 Kết nối tri thức Bài 19: Phương trình đường thẳng

Bài 7.7 trang 31 Sách bài tập Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác ABC có toạ độ ba đỉnh A(0; –1), B(2; 3) và C(–4; 1). Lập phương trình tham số của đường trung bình ứng với cạnh BC của tam giác ABC.

Lời giải:

Gọi d là đường trung bình ứng với cạnh BC của tam giác ABC nên d // BC và d đi qua trung điểm M của AB, do đó:

Đường thẳng d nhận vectơ $\overrightarrow{BC}$ = (–4 – 2; 1 – 3) = (–6; –2) là một vectơ chỉ phương.

Tọa độ trung điểm M là x_M = $\frac{0+2}{2}=1$; y_M = $\frac{(-1)+3}{2}=1$.

Suy ra M(1; 1) thuộc d.

Phương trình tham số của d là: