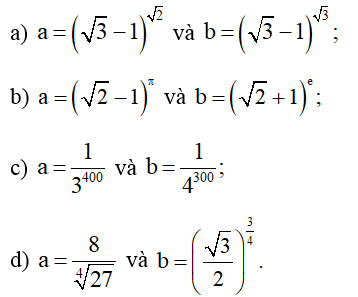Không sử dụng máy tính cầm tay, so sánh hai số a và b, biết
Không sử dụng máy tính cầm tay, so sánh hai số a và b, biết:
Giải sách bài tập Toán 11 Bài 1: Phép tính lũy thừa với số mũ thực
Bài 12 trang 34 SBT Toán 11 Tập 2: Không sử dụng máy tính cầm tay, so sánh hai số a và b, biết:
Lời giải:
a) Do và nên
Suy ra: a > b.
b) Ta có:
Do và –π < e nên ta có:
Suy ra: a < b.
c) Ta có: và
Do 100 > 0 và nên
Suy ra: a < b.
d) Ta có:
Do và nên
Suy ra: a > b.
Lời giải SBT Toán 11 Bài 1: Phép tính lũy thừa với số mũ thực hay khác:
Bài 1 trang 33 SBT Toán 11 Tập 2: Điều kiện xác định của x–7 là: ....
Bài 2 trang 34 SBT Toán 11 Tập 2: Điều kiện xác định của là:....
Bài 3 trang 34 SBT Toán 11 Tập 2: Điều kiện xác định của là:....
Bài 4 trang 34 SBT Toán 11 Tập 2: Điều kiện xác định của là:....
Bài 5 trang 34 SBT Toán 11 Tập 2: Giá trị của biểu thức bằng:....
Bài 9 trang 34 SBT Toán 11 Tập 2: Biểu thức với x > 0 được rút gọn bằng:....
Bài 10 trang 34 SBT Toán 11 Tập 2: Biểu thức với a > 0 được rút gọn bằng:....
Bài 11 trang 34 SBT Toán 11 Tập 2: Viết các biểu thức sau về lũy thừa cơ số a, biết:....
Bài 13 trang 35 SBT Toán 11 Tập 2: Xác định các giá trị của số thực a thỏa mãn:....
Bài 14 trang 35 SBT Toán 11 Tập 2: Cho a > 0, b > 0. Rút gọn mỗi biểu thức sau:....
Bài 15 trang 35 SBT Toán 11 Tập 2: Cho x, y là các số thực dương và số thực a thỏa mãn: ....