Cho hình chóp tứ giác S.ABCD. Gọi G, K lần lượt là trọng tâm của các tam giác SAB và SAD

Cho hình chóp tứ giác S.ABCD. Gọi G, K lần lượt là trọng tâm của các tam giác SAB và SAD; M, N lần lượt là trung điểm của BC và CD. Chứng minh rằng GK // MN.

Giải SBT Toán 11 Cánh diều Bài 2: Hai đường thẳng song song trong không gian

Bài 17 trang 100 SBT Toán 11 Tập 1: Cho hình chóp tứ giác S.ABCD. Gọi G, K lần lượt là trọng tâm của các tam giác SAB và SAD; M, N lần lượt là trung điểm của BC và CD. Chứng minh rằng GK // MN.

Lời giải:

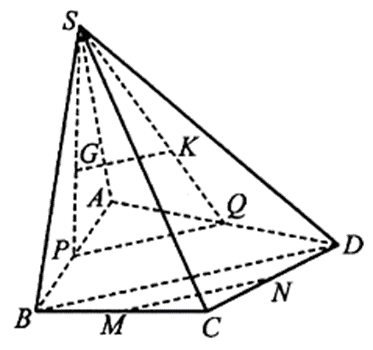
Gọi P, Q lần lượt là trung điểm của AB và AD.

Vì G là trọng tâm của tam giác SAB nên $\frac{SG}{SP}=\frac{2}{3}$.

Vì K là trọng tâm của tam giác SAD nên $\frac{SK}{SQ}=\frac{2}{3}$.

Khi đó, ta có $\frac{SG}{SP}=\frac{SK}{SQ}$, suy ra GK // PQ. (1)

Vì PQ là đường trung bình của tam giác ABD nên PQ // BD;

MN là đường trung bình của tam giác BCD nên MN // BD.

Suy ra MN // PQ. (2)

Từ (1) và (2) suy ra GK // MN.

Lời giải Sách bài tập Toán lớp 11 Bài 2: Hai đường thẳng song song trong không gian hay khác:

• Bài 10 trang 99 SBT Toán 11 Tập 1: Hai đường thẳng chéo nhau khi và chỉ khi ....

• Bài 11 trang 99 SBT Toán 11 Tập 1: Cho ba đường thẳng a, b, c. Trong các mệnh đề sau, mệnh đề nào đúng? ....

• Bài 12 trang 100 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC ....

• Bài 13 trang 100 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, AD. Giao tuyến của hai mặt phẳng (CMN) và (BCD) là đường thẳng song song với đường thẳng nào sau đây? ....

• Bài 14 trang 100 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD ....

• Bài 15 trang 100 SBT Toán 11 Tập 1: Quan sát hình căn phòng (Hình 16), hãy cho biết vị trí tương đối của các cặp đường thẳng a và b; a và c; b và c ....

• Bài 16 trang 100 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD và P là một điểm nằm trên CD ....

• Bài 18 trang 100 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, K, L lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SAD ....