Cho dãy số (un), biết u1 = – 2 trang 57 SBT Toán 11
Giải sách bài tập Toán 11 Bài tập cuối chương 2
Bài 57 trang 57 SBT Toán 11 Tập 1: Cho dãy số (un), biết u1 = – 2, với n ∈ ℕ*. Đặt với n ∈ ℕ*.
a) Chứng minh rằng dãy số (vn) là cấp số nhân. Tìm số hạng đầu, công bội của cấp số nhân đó.
b) Tìm công thức của un tính theo n.
Lời giải:
a) Ta có ;
với mọi n ∈ ℕ*.
Vậy dãy số (vn) là một cấp số nhân có số hạng đầu v1 = – 2 và công bội .
b) Từ kết quả của câu a) suy ra .
Từ , suy ra với mọi n ≥ 2.
Lời giải Sách bài tập Toán lớp 11 Bài tập cuối chương 2 Cánh diều hay khác:
Bài 47 trang 56 SBT Toán 11 Tập 1: Cho dãy số (un) biết un = 5n – n. Số hạng un + 1 là: ....
Bài 48 trang 56 SBT Toán 11 Tập 1: Cho dãy số (un) biết u1 = 2, với n ≥ 2. Số hạng u4 bằng: ....

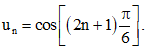 ....
....