Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD
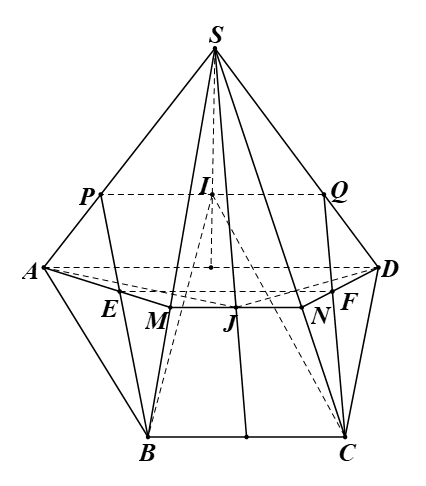
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q.
Giải sách bài tập Toán 11 Bài 2: Hai đường thẳng song song - Chân trời sáng tạo
Bài 1 trang 117 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q.
a) Chứng minh MN song song với PQ.
b) Gọi E là giao điểm của AM và BP, F là giao điểm của CQ và DN. Chứng minh EF song song với MN và PQ.
Lời giải:
a) • ABCD là hình thang nên AD // BC
Ta có: M ∈ SB, mà SB ⊂ (SBC) nên M ∈ (SBC);
M ∈ (ADJ)
Do đó M ∈ (ADJ) ∩ (SBC).
Tương tự, N ∈ (ADJ) ∩ (SBC).
Suy ra (ADJ) ∩ (SBC) = MN
Mà AD // BC; AD ⊂ (ADJ); BC ⊂ (SBC);
Suy ra MN // AD // BC. (1)
• Chứng minh tương tự như trên, ta cũng có PQ // AD // BC. (2)
Từ (1), (2) suy ra MN // PQ.
b) Ta có: E ∈ AM, mà AM ⊂ (ADJ) nên E ∈ (ADJ);
E ∈ BP, mà BP ⊂ (IBC) nên E ∈ (IBC).
Do đó E ∈ (ADJ) ∩ (IBC).
Tương tự ta cũng có F ∈ (ADJ) ∩ (IBC).
Suy ra (ADJ) ∩ (IBC) = EF.
Mà AD // BC, AD ⊂ (ADJ), BC ⊂ (IBC).
Suy ra EF // AD // BC
Lại có MN // PQ // AD // BC (chứng minh câu a)
Do đó EF // MN // PQ.
Lời giải Sách bài tập Toán lớp 11 Bài 2: Hai đường thẳng song song hay khác: