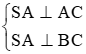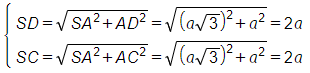Cho hình chóp S ABCD có đáy là hình thoi cạnh a SA =a căn bậc hai 3 SA ⊥ AC

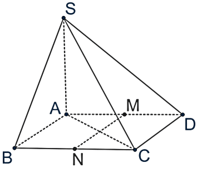
Cho hình chóp S.ABCD. có đáy là hình thoi cạnh a, SA = , SA AC, SA BC, = 120°. Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:

Giải sách bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc - Chân trời sáng tạo

Bài 2 trang 51 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD. có đáy là hình thoi cạnh a, SA = $a\sqrt{3}$, SA $\perp$ AC, SA $\perp$ BC, $\widehat{BAD}$= 120°. Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:

a) SD và BC.

b) MN và SC.

Lời giải:

a) Ta có:

$\Rightarrow$ SA ⊥ (ABCD) $\iff$ SA ⊥ AD.

Do BC // AD nên (BC, SD) = (AD, SD).

$\tan \widehat{ADS}=\frac{SA}{AD}=\frac{a\sqrt{3}}{a}=\sqrt{3}$

Do đó $\left(BC,SD\right)=\widehat{ADS}$ = 60°.

b) Do MN // CD nên (SD, MN) = (SD, CD) = $\widehat{SCD}$ .

Áp dụng định lí Pythagore, ta có:

Áp dụng định lí hàm cos trong ∆SCD, ta có:

$\cos \widehat{SCD}=\frac{S{C}^2+C{D}^2-S{D}^2}{2.SC.CD}=\frac{{\left(2a\right)}^2+a^2-{\left(2a\right)}^2}{2.2.a.a}=\frac{1}{4}$.

Do đó (SD, MN) =  ≈ 75,52°.

Lời giải SBT Toán 11 Bài 1: Hai đường thẳng vuông góc hay khác:

• Bài 1 trang 50 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Tính góc giữa AB và DM. ....

• Bài 3 trang 51 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AB = CD, AC = BD, AD = BC. a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó. ....

• Bài 4 trang 51 SBT Toán 11 Tập 2: Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của ....

• Bài 5 trang 51 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh hai đường thẳng ....