Cho tứ diện đều ABCD cạnh a Gọi O là tâm đường tròn ngoại tiếp tam giác BCD

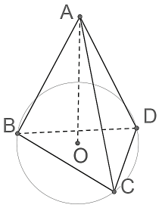
Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh hai đường thẳng OA và CD vuông góc với nhau.

Giải sách bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc - Chân trời sáng tạo

Bài 5 trang 51 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh hai đường thẳng OA và CD vuông góc với nhau.

Lời giải:

Giả sử điểm H là chân đường vuông góc hạ từ đỉnh A xuống mặt phẳng đáy.

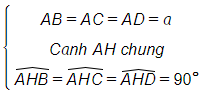
Xét ∆AHB, ∆AHC và ∆AHD:

$\Rightarrow$ ∆AHB, ∆AHC và ∆AHD là các tam giác bằng nhau (cạnh huyền – cạnh góc vuông).

$\Rightarrow$ BH = CH = DH    $\Rightarrow$ H là tâm đường tròn ngoại tiếp tam giác BCD.

$\Rightarrow$ H $\equiv$ O$\iff$ AO là đường cao của tứ diện ABCD.

$\Rightarrow$ OA ⊥ CD.

Vậy hai đường thẳng OA và CD vuông góc với nhau.

Lời giải SBT Toán 11 Bài 1: Hai đường thẳng vuông góc hay khác:

• Bài 1 trang 50 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Tính góc giữa AB và DM. ....

• Bài 2 trang 51 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD. có đáy là hình thoi cạnh a, SA = $a\sqrt{3}$, SA $\perp$ AC, SA $\perp$ BC, $\widehat{BAD}$ = 120°. Gọi M, N lần lượt ....

• Bài 3 trang 51 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AB = CD, AC = BD, AD = BC. a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó. ....

• Bài 4 trang 51 SBT Toán 11 Tập 2: Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của ....