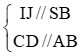Cho hình chóp tứ giác S ABCD có tất cả các cạnh đều bằng a Gọi M N I J lần lượt là

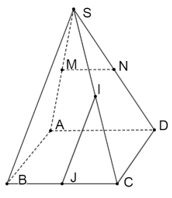
Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính góc giữa các cặp đường thẳng sau:

Giải sách bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc - Chân trời sáng tạo

Bài 4 trang 51 SBT Toán 11 Tập 2: Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N, I, J lần lượt là trung điểm của SA, SD, SC và BC. Tính góc giữa các cặp đường thẳng sau:

a) IJ và DC;

b) MN và IJ.

Lời giải:

a) Ta có:

$\Rightarrow (IJ,CD)=(SB,AB)=\widehat{SBA}$.

Từ giả thiết, ta có ∆SAB là tam giác đều.

$\Rightarrow (IJ,CD)=\widehat{SBA}=60°$.

b)Ta có:

$\Rightarrow (IJ,MN)=(SB,BC)=\widehat{SBC}$.

Từ giả thiết, ta có ∆SBC là tam giác đều.

Do đó $(IJ,MN)=\widehat{SBC}=60°$ .

Lời giải SBT Toán 11 Bài 1: Hai đường thẳng vuông góc hay khác:

• Bài 1 trang 50 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Tính góc giữa AB và DM. ....

• Bài 2 trang 51 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD. có đáy là hình thoi cạnh a, SA = $a\sqrt{3}$, SA $\perp$ AC, SA $\perp$ BC, $\widehat{BAD}$ = 120°. Gọi M, N lần lượt ....

• Bài 3 trang 51 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AB = CD, AC = BD, AD = BC. a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó. ....

• Bài 5 trang 51 SBT Toán 11 Tập 2: Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh hai đường thẳng ....