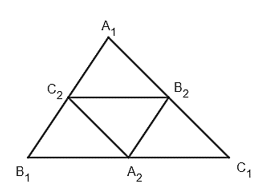
Cho tam giác A1B1C1 có diện tích là 3 (đơn vị diện tích)

Cho tam giác ABC có diện tích là 3 (đơn vị diện tích). Dựng tam giác ABC bằng cách nối các trung điểm của các cạnh BC, CA, AB. Tiếp tục quá trình này, ta có các tam giác ABC, ..., ABC,... Kí hiệu s là diện tích của tam giác ABC.

Giải sách bài tập Toán 11 Bài 15: Giới hạn của dãy số - Kết nối tri thức

Bài 5.8 trang 78 SBT Toán 11 Tập 1: Cho tam giác A₁B₁C₁ có diện tích là 3 (đơn vị diện tích). Dựng tam giác A₂B₂C₂ bằng cách nối các trung điểm của các cạnh B₁C₁, C₁A₁, A₁B₁. Tiếp tục quá trình này, ta có các tam giác A₃B₃C₃, ..., A_nB_nC_n,... Kí hiệu s_n là diện tích của tam giác A_nB_nC_n.

a) Tính s_n.

b) Tính tổng s₁ + s₂ + ... + s_n + ...

Lời giải:

a)

Theo cách xác định tam giác A₂B₂C₂, ta có s₂ = $\frac{1}{4}$ s₁.

Tương tự, s₃ = $\frac{1}{4}$ s₂, ...., $s_n=\frac{1}{4}{s}_{n-1}$ .

Vậy $s_n={\left(\frac{1}{4}\right)}^{n-1}{s}_1={\left(\frac{1}{4}\right)}^{n-1}.3=3{\left(\frac{1}{4}\right)}^{n-1}$ .

b) Ta có s₁ + s₂ + ... + s_n + ... là tổng của cấp số nhân lùi vô hạn có số hạng đầu u₁ = 3 và công bội q = $\frac{1}{4}$ . Do đó

s₁ + s₂ + ... + s_n + ... = $\frac{3}{1-\frac{1}{4}}=4$ .

Lời giải SBT Toán 11 Bài 15: Giới hạn của dãy số hay khác:

• Bài 5.1 trang 77 SBT Toán 11 Tập 1: Tính các giới hạn sau: ....

• Bài 5.2 trang 78 SBT Toán 11 Tập 1: Tính các giới hạn sau: ....

• Bài 5.3 trang 78 SBT Toán 11 Tập 1: Cho $u_n=\frac{1+a+a^2+\mathrm{...}+a^n}{1+b+b^2+\mathrm{...}+b^n}$ với a, b là các số thực thỏa mãn |a| < 1, |b| < 1. Tính $\underset{n\to +\infty }{\lim }{u}_n$ . ....

• Bài 5.4 trang 78 SBT Toán 11 Tập 1: Tính $\underset{n\to +\infty }{\lim }\frac{1+3+5+\mathrm{...}+\left(2n-1\right)}{n^2+2n}$....

• Bài 5.5 trang 78 SBT Toán 11 Tập 1: Tính tổng $S=-1+\frac{1}{5}-\frac{1}{5^2}+\mathrm{...}+{\left(-1\right)}^n\frac{1}{5^{n-1}}$ + … ....

• Bài 5.6 trang 78 SBT Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số: ....

• Bài 5.7 trang 78 SBT Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{\cos n}{n^2}$. Tính $\underset{n\to +\infty }{\lim }{u}_n$. ....

• Bài 5.9 trang 78 SBT Toán 11 Tập 1: Cho dãy số (u_n) với u₁ = 2, $u_{n+1}=u_n+\frac{2}{3^n}$, n ≥ 1. Đặt v_n = u_{n + 1} – u_n ....

• Bài 5.10 trang 78 SBT Toán 11 Tập 1: Cho dãy số (u_n) có tính chất $\left|u_n-\frac{n}{n+1}\right|\le \frac{1}{n^2}$. Tính $\underset{n\to +\infty }{\lim }{u}_n$. ....