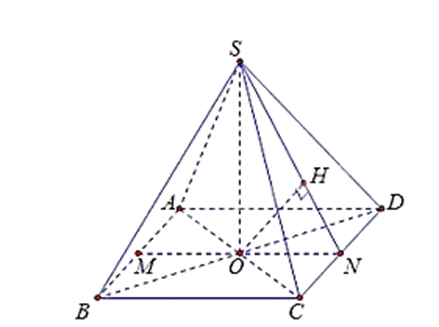
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD

❮ Bài trước Bài sau ❯

Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD. Khoảng cách giữa hai đường thẳng AB và SD bằng

Giải sách bài tập Toán 11 Bài tập cuối chương 7 - Kết nối tri thức

Bài 7.47 trang 42 SBT Toán 11 Tập 2: Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD. Khoảng cách giữa hai đường thẳng AB và SD bằng

A. $\frac{a \sqrt{3}}{3}$ .

B. $\frac{a \sqrt{3}}{2}$ .

C. $\frac{a \sqrt{6}}{3}$ .

D. $\frac{a \sqrt{6}}{2}$ .

Lời giải:

Đáp án đúng là: C

Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a, gọi O là giao điểm của AC và BD

Gọi M và N lần lượt là trung điểm của AB và CD. Vì ABCD là hình vuông nên O là trung điểm của AC, BD, MN.

Vì ABCD là hình vuông nên AB // CD suy ra AB // (SCD).

Khi đó d(AB, SD) = d(AB, (SCD)) = d(M, (SCD)) = 2 . d(O, (SCD)).

Ta có SO $⊥$ (ABCD) nên SO $⊥$ CD mà CD $⊥$ ON (do MN // BC) nên CD $⊥$ (SON).

Hạ OH $⊥$ SN tại H, OH $⊥$ CD (do CD $⊥$ (SON)) nên OH $⊥$ (SCD).

Do đó d(O, (SCD)) = OH.

Xét tam giác BCD có ON là đường trung bình nên ON = $\frac{B C}{2} = \frac{a}{2}$ .

Xét tam giác ABC vuông tại B, có AC = $\sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ .

ABCD là hình vuông, O là giao điểm của AC và BD nên O là trung điểm của AC, suy ra OC = $\frac{A C}{2} = \frac{a \sqrt{2}}{2}$ .

Xét tam giác SOC vuông tại O có: SO = $\sqrt{S C^{2} - O C^{2}} = \sqrt{a^{2} - \frac{2 a^{2}}{4}} = \frac{a \sqrt{2}}{2}$ .

Xét tam giác SON vuông tại O, OH là đường cao, ta có

$\frac{1}{O H^{2}} = \frac{1}{S O^{2}} + \frac{1}{O N^{2}}$ $= \frac{4}{2 a^{2}} + \frac{4}{a^{2}} = \frac{6}{a^{2}}$ $\Rightarrow O H = \frac{a \sqrt{6}}{6}$ .

Vậy d(AB, SD) = 2 . OH = $\frac{a \sqrt{6}}{3}$ .

Lời giải SBT Toán 11 Bài tập cuối chương 7 hay khác:

Xem thêm lời giải Sách bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯