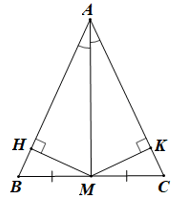
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác góc A

Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác góc A. Chứng minh tam giác ABC là tam giác cân.

Giải sách bài tập Toán lớp 7 Bài 7: Tính chất ba đường trung tuyến của tam giác

Bài 2 trang 60 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác góc A. Chứng minh tam giác ABC là tam giác cân.

Lời giải:

Vẽ đường cao MH của tam giác AMB và vẽ đường cao MK của tam giác AMC.

• Xét ∆AMH và ∆AMK có:

$\widehat{AHM}=\widehat{AKM}\left(=90°\right)$,

AM là cạnh chung,

$\widehat{HAM}=\widehat{K\text{A}M}$ (vì AM là tia phân giác của $\widehat{BAC}$).

Do đó ∆AMH = ∆AMK (cạnh huyền – góc nhọn).

Suy ra MH = MK (hai cạnh tương ứng).

• Xét ∆BMH và ∆CMK có:

$\widehat{BHM}=\widehat{CKM}\left(=90°\right)$,

MH = MK (chứng minh trên),

BM = CM (vì AM là trung tuyến của tam giác ABC).

Do đó ∆BMH = ∆CMK (cạnh huyền – cạnh góc vuông).

Suy ra $\hat{B}=\hat{C}$ (hai góc tương ứng).

Xét tam giác ABC có $\hat{B}=\hat{C}$ nên tam giác ABC cân tại A.

Vậy ABC là tam giác cân tại A.