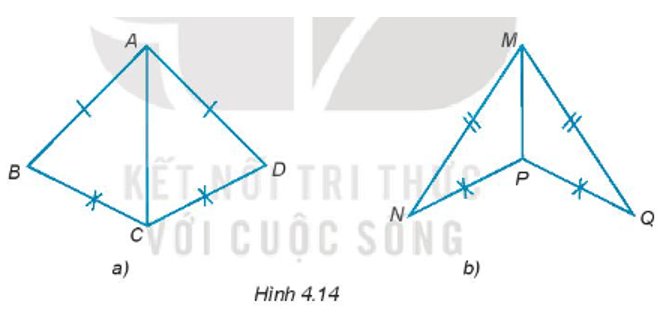
Cho Hình 4.14, chứng minh rằng ∆ABC = ∆ADC; ∆MNP = ∆MQP
Cho Hình 4.14, chứng minh rằng ∆ABC = ∆ADC; ∆MNP = ∆MQP.
Giải SBT Toán 7 Kết nối tri thức Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Bài 4.15 trang 57 sách bài tập Toán lớp 7 Tập 1: Cho Hình 4.14, chứng minh rằng ∆ABC = ∆ADC; ∆MNP = ∆MQP.
Lời giải:
a) Xét ∆ABC và ∆ADC có:
AB = AD (giả thiết)
BC = DC (giả thiết)
AC chung
Do đó, ∆ABC = ∆ADC (c – c – c).
b) Xét ∆MNP và ∆MQP có:
MP chung
NP = PQ (giả thiết)
MN = MQ (giả thiết)
Do đó, ∆MNP = ∆MQP (c – c – c).