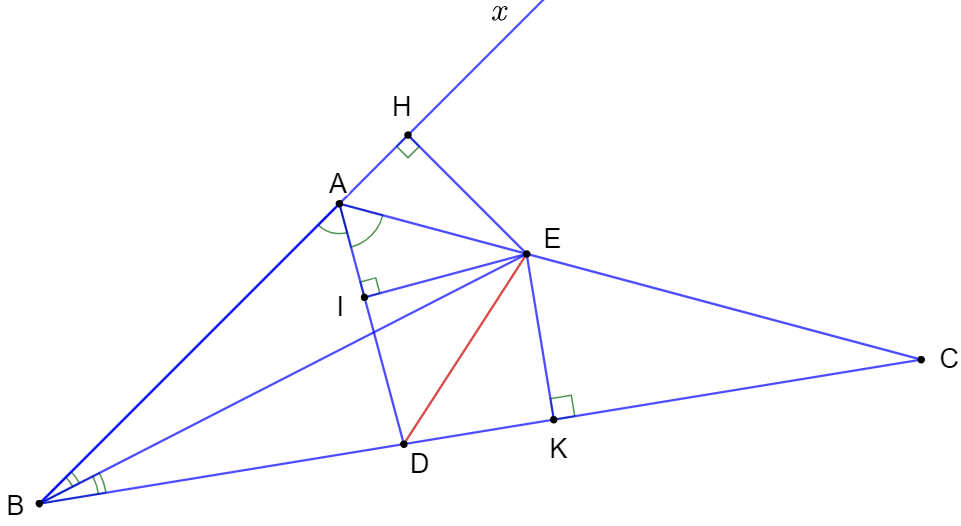
Tam giác ABC có AD, BE là hai đường phân giác và góc BAC = 120 độ

Giải SBT Toán 7 Kết nối tri thức Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Bài 9.17 trang 55 sách bài tập Toán lớp 7 Tập 2: Tam giác ABC có AD, BE là hai đường phân giác và $\widehat{BAC}=120°$. Chứng minh rằng DE là tia phân giác của góc ADC.

Lời giải:

Gọi Ax là tia đối của tia AB thì ba góc BAD, DAC, CAx có cùng số đo 60º.

Hạ EH ⏊ Bx, EI ⏊ AD, EK ⏊ BC.

Ta có: Vì BE là phân giác góc ABC nên suy ra EH = EK (Áp dụng định lí 2).

Vì AE là phân giác góc DAx nên suy ra EH = EI (Áp dụng định lí 2).

Suy ra EK = EI hay E nằm trên tia phân giác của ADC.

Vậy suy ra DE là đường phân giác của góc ADC (đpcm).