Cho tam giác ABC với AB > AC. Gọi M là trung điểm của cạnh BC

Giải SBT Toán 7 Kết nối tri thức Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác

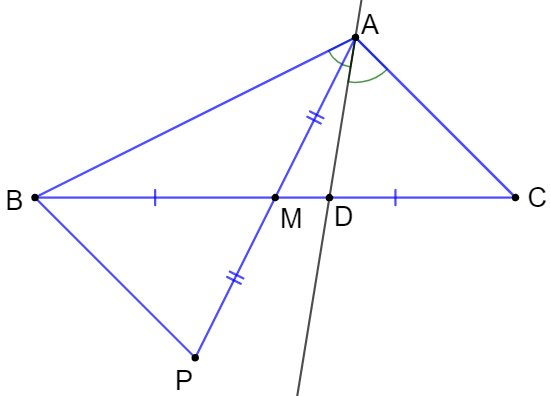
Bài 9.4 trang 48 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC với AB > AC. Gọi M là trung điểm của cạnh BC.

a) Hãy so sánh hai góc MAB và MAC.

(HD. Lấy điểm P sao cho M là trung điểm của AP rồi chứng minh hai tam giác AMC và PMB bằng nhau).

b) Tia phân giác của góc BAC cắt BC tại D. Hỏi D thuộc đoạn thẳng MB hay đoạn thẳng MC? Vì sao?

Lời giải:

Cho tam giác ABC với AB > AC. Gọi M là trung điểm của cạnh BC

a) Lấy P là điểm thuộc đường thẳng AM sao cho M là trung điểm của AP.

Xét hai tam giác ∆ AMC và ∆ PMB có:

AM = PM (M là trung điểm của AP)

MC = MB (M là trung điểm của BC)

$\hat{A M C} = \hat{P M B}$ (hai góc đối đỉnh)

Do đó ∆AMC = ∆PMB (c.g.c)

Suy ra $\hat{M A C} = \hat{M P B}$ (hai góc tương ứng) (1)

Và AC = PB

Mà AB > AC (gt)

Nên suy ra AB > PB

Xét tam giác ABP có AB > PB (cmt) nên theo định lí 1 ta có $\hat{A P B} > \hat{B A P}$ (2)

Từ (1) và (2) suy ra $\hat{M A C} > \hat{M A B}$ (3).

b) AD là đường phân giác của góc BAC nên ta có: $\hat{B A D} = \hat{D A C}$ (4)

Từ (3) và (4) nên suy ra được: $2 \hat{M A C} > \hat{M A C} + \hat{M A B} = \hat{B A C}$

Hay $2 \hat{M A C} > \hat{D A B} + \hat{D A C} = 2 \hat{D A C}$

Suy ra $\hat{M A C} > \hat{D A C}$ .

Do đó MC > DC.

Vậy D là điểm thuộc đoạn thẳng MC.