Giải SBT Toán 7 trang 43 Tập 1 Kết nối tri thức

Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 43 Tập 1 trong Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 43.

Giải SBT Toán 7 trang 43 Tập 1 Kết nối tri thức

Bài 3.21 trang 43 sách bài tập Toán lớp 7 Tập 1:

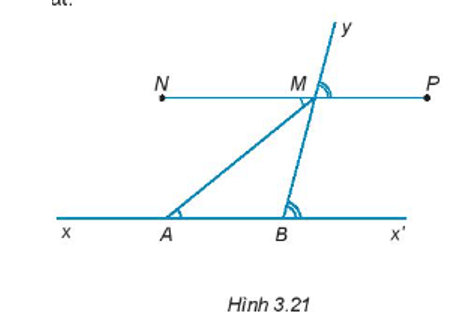
Cho đường thẳng xx’, điểm A thuộc xx’. Trên tia Ax’ lấy điểm B (điểm B khác điểm A). Vẽ tia By, trên tia By lấy điểm M. Hai điểm N và P thảo mãn: $\widehat{NMA}$ = $\widehat{MAB}$; $\widehat{PMy}= \widehat{MBx\text{'}}$(H.3.21) Giải thích tại sao ba điểm N; M; P thẳng hàng.

Lời giải:

Theo đề bài ra ta có:

$\widehat{NMA}= \widehat{MAB}$, mà hai góc này ở vị trí so le trong, suy ra MN // xx;

$\widehat{PMy}=\widehat{MBx\text{'}}$, mà hai góc này ở vị trí đồng vị, suy ra MP // xx’

Theo tiên đề Euclid, qu điểm M chỉ có một đường thẳng song song với xx’. Mà MN và NP cùng song song với xx’ nên MN vag MP trùng nhau.

Do đó, ba điểm M, N, P thẳng hàng.

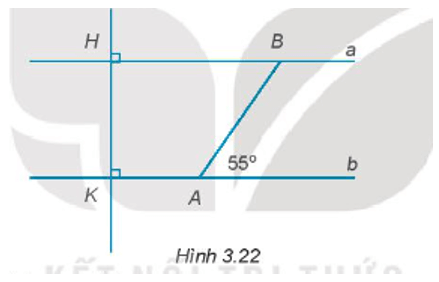
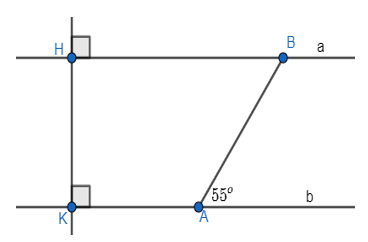
Bài 3.22 trang 43 sách bài tập Toán lớp 7 Tập 1: Vẽ lại Hình 3.22 vào vở.

a) Giải thích tại sao a // b.

b) Tính số đo góc ABH.

Lời giải:

a) Vì HK vuông góc với a tại H; HK vuông góc với b tại K nên a // b (quan hệ từ vuông góc đến song song).

b) Vì a // b nên các góc so le trong bằng nhau và các góc đồng vị bằng nhau.

Lại có: $\widehat{ABH}$ và $\widehat{BAb}$ là hai góc so le trong.

Do đó, $\widehat{ABH}= \widehat{BAb}$ = 55^o.

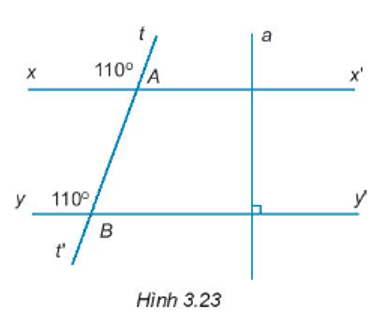
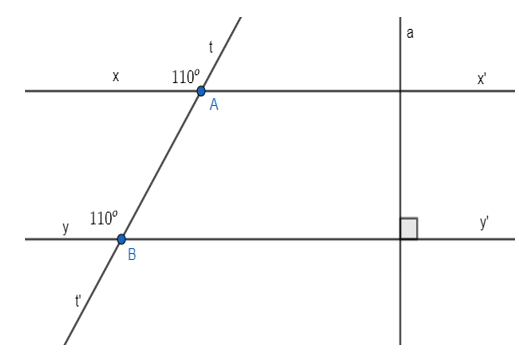
Bài 3.23 trang 43 sách bài tập Toán lớp 7 Tập 1: Vẽ lại Hình 3.23 vào vở. Giải thích tại sao

a) xx’ // yy’.

b) xx’ a.

Lời giải:

a) Ta có: $\widehat{tAx}$ = 110^o và $\widehat{yBt}$ = 110^o nên $\widehat{tAx}$ = $\widehat{yBt}$ = 110^o. Mà hai góc này ở vị trí đồng vị. Do đó, xx’ song song với yy’.

b) Vì a vuông góc với yy’ mà yy’ lại song song với xx’ nên a vuông góc với xx’.

Lời giải sách bài tập Toán lớp 7 Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song Kết nối tri thức hay khác:

• Giải SBT Toán 7 trang 42 Tập 1

• Giải SBT Toán 7 trang 44 Tập 1