Giải SBT Toán 7 trang 64 Tập 1 Kết nối tri thức

❮ Bài trước Bài sau ❯

Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 64 Tập 1 trong Bài 15: Các trường hợp bằng nhau của tam giác vuông Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 64.

Giải SBT Toán 7 trang 64 Tập 1 Kết nối tri thức

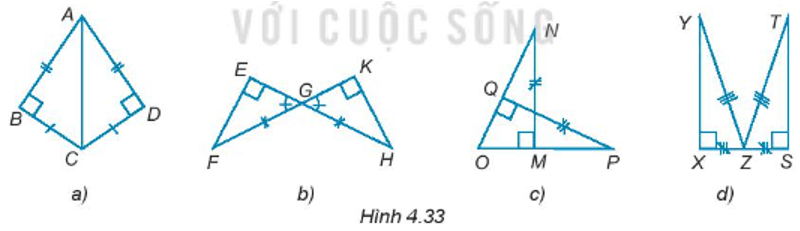
Bài 4.31 trang 64 sách bài tập Toán lớp 7 Tập 1: Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau?

Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau

Lời giải:

+) Hình a:

Xét ∆ABC và ∆ADC ta có:

AB = AD (giả thiết)

$\hat{A B C} = \hat{A D C}$ = 90° (giả thiết)

BC = CD (giả thiết)

Do đó, ∆ABC = ∆ADC (hai cạnh góc vuông).

+) Hình b

Xét ∆EFG và ∆KHG ta có:

GF = GH (giả thiết)

$\hat{F E G} = \hat{H K G}$ = 90° (giả thiết)

$\hat{E G F} = \hat{H G K}$ = (hai góc đối đỉnh)

Do đó, ∆EFG = KHG (góc nhọn – cạnh huyền)

+) Hình c:

Tam giác OMN vuông tại M nên $\hat{O N M} + \hat{O} = 90 ° \Rightarrow \hat{O N M} = 90 ° - \hat{O} .$

Tam giác OQP vuông tại Q nên $\hat{O P Q} + \hat{O} = 90 ° \Rightarrow \hat{O P Q} = 90 ° - \hat{O} .$

Do đó, $\hat{O N M} = \hat{O P Q}$ .

Xét ∆OMN và ∆OQP ta có:

MN = PQ (giả thiết)

$\hat{O M N} = \hat{O Q P}$ = 90^o (giả thiết)

$\hat{O N M} = \hat{O P Q}$ (chứng minh trên)

Do đó, ∆OMN = ∆OQP (góc nhọn – cạnh góc vuông).

+) Hình d:

Xét ∆XYZ và ∆STZ ta có:

YZ = TZ (giả thiết)

$\hat{Y X Z} = \hat{T S Z}$ = 90° (giả thiết)

XZ = SZ (giả thiết)

Do đó, ∆XYZ = ∆STZ (cạnh huyền – cạnh góc vuông).

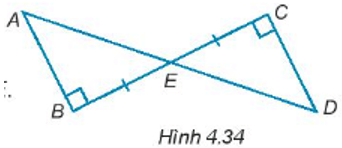
Bài 4.32 trang 64 sách bài tập Toán lớp 7 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh rằng ∆ABE = ∆DCE.

Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC