Giải SBT Toán 7 trang 68 Tập 1 Kết nối tri thức

---

Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 68 Tập 1 trong Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 68.

Giải SBT Toán 7 trang 68 Tập 1 Kết nối tri thức

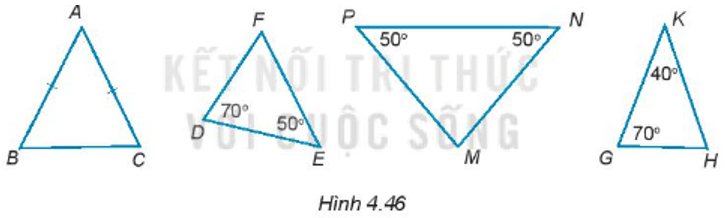
Bài 4.41 trang 68 sách bài tập Toán lớp 7 Tập 1: Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại đỉnh nào? Vì sao?

Lời giải:

+ Tam giác ABC có AB = AC (kí hiệu bằng nhau trên hình)

Do đó, tam giác ABC cân tại đỉnh A.

+ Áp dụng định lí tổng 3 góc trong tam giác DEF, ta có:

$\hat{D}+\hat{E}+\hat{F}=180°$

Suy ra $\hat{F}=180°-\left(\begin{array}{cc}\hat{D}+& \hat{E}\end{array}\right) =180°-(70°+50°)=60°$.

Do đó ta có, $\hat{D}\ne \hat{E}\ne \hat{F}$. Vậy tam giác DEF không phải tam giác cân.

+ Tam giác MNP có $\hat{N}=\hat{P}(=50°)$.

Do đó, tam giác MNP cân tại đỉnh M.

+ Áp dụng định lí tổng 3 góc trong tam giác KGH, ta có:

$\hat{K}+\hat{G}+\hat{H}=180°$

Suy ra $\hat{H}=180°-(\hat{K}+\hat{G})=180°-(40°+70°)=70°$.

Do đó tam giác KGH có $\hat{G}=\hat{H}=70°$.

Vậy tam giác KGH cân tại đỉnh K.

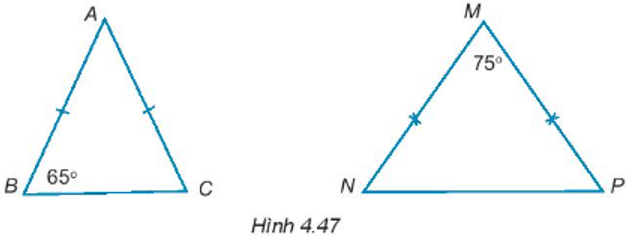
Bài 4.42 trang 68 sách bài tập Toán lớp 7 Tập 1: Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).

Lời giải:

+ Tam giác ABC có AB = AC nên tam giác ABC cân tại đỉnh A.

Suy ra $\hat{C}=\hat{B}=65°$.

Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:

$\hat{A}+\hat{B}+\hat{C}=180°$

Suy ra $\hat{A}=180°-\left(\begin{array}{cc}\hat{B}+& \hat{C}\end{array}\right)=180°-(65°-65°)=50°$.

+ Tam giác MNP có MN = MP nên tam giác MNP cân tại đỉnh M.

Suy ra $\hat{M}=\hat{N}$.

Áp dụng định lí tổng ba góc trong tam giác MNP, ta có:

$\hat{M}+\hat{N}+\hat{P}=180°$

$\Rightarrow \hat{M}+\hat{M}=180°-\hat{P}\Rightarrow 2\hat{M}=180°-\hat{P}$

$\Rightarrow \hat{M}=\frac{180°-\hat{P}}{2}=\frac{180°-75°}{2}=52,5°.$

Vậy $\hat{M}=\hat{N}=52,5°.$ 

Lời giải sách bài tập Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Kết nối tri thức hay khác:

• Giải SBT Toán 7 trang 69 Tập 1

• Giải SBT Toán 7 trang 70 Tập 1