Giải SBT Toán 7 trang 70 Tập 1 Kết nối tri thức

---

Haylamdo sưu tầm và biên soạn Giải SBT Toán 7 trang 70 Tập 1 trong Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Sách bài tập Toán lớp 7 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 70.

Giải SBT Toán 7 trang 70 Tập 1 Kết nối tri thức

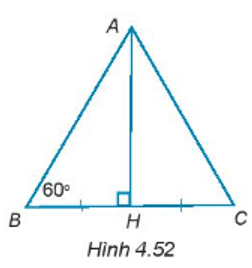
Bài 4.47 trang 70 sách bài tập Toán lớp 7 Tập 1: Cho tam giác ABH vuông tại đỉnh H có $\widehat{ABH}=60°$. Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng ∆ABC là tam giác đều và BH = $\frac{AB}{2}$.

Lời giải:

+ Xét tam giác vuông ABH và tam giác vuông ACH có:

AH: cạnh chung

HB = HC (gt)

Do đó, ∆ABH = ∆ACH (hai cạnh góc vuông).

Suy ra AB = AC.   (1)

Do đó, tam giác ABC cân tại đỉnh A.

⇒$\hat{C}=\hat{B}=\widehat{ABH}=60°$.

Ta có: $\widehat{BAC}+\hat{B}+\hat{C}=180°$ (định lí tổng ba góc trong tam giác).

Suy ra $\widehat{BAC}=180°-\hat{B}-\hat{C}=180°-60°-60°=60°$.

Khi đó $\hat{B}=\widehat{BAC}$, do đó tam giác ABC cân tại đỉnh C nên  AC = BC. (2)

Từ (1) và (2) suy ra AB = AC = BC.

Do đó, ∆ABC đều.

+ Vì H thuộc BC và điểm H nằm giữa điểm B và điểm C, hơn nữa HB = HC, do đó H là trung điểm của BC.

Suy ra $BH=\frac{BC}{2}$.

Mà BC = AB (chứng minh trên).

Vậy BH = $\frac{AB}{2}$.

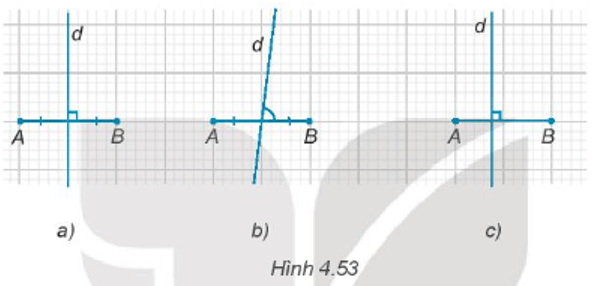
Bài 4.48 trang 70 sách bài tập Toán lớp 7 Tập 1: Đường thẳng d trong hình nào dưới đây là trung trực của đoạn thẳng AB?

Lời giải:

Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.

Do đó, trong các Hình 4.53, chỉ có đường thẳng d trong Hình 4.53a là đường trung trực của đoạn thẳng.

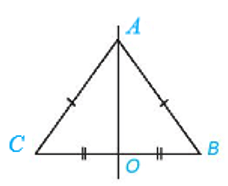
Bài 4.49 trang 70 sách bài tập Toán lớp 7 Tập 1: Cho A là một điểm tùy ý nằm trên đường trung trực của đoạn thẳng BC sao cho A không thuộc BC. Khẳng định nào dưới đây là đúng?

a) AB = AC.

b) Tam giác ABC đều.

c) $\widehat{ABC}=\widehat{ACB}$.

d) Tam giác ABC cân tại đỉnh A.

Lời giải:

Điểm A thuộc đường trung trực của BC nên AB = AC (điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó).

Do đó, ∆ABC cân tại đỉnh A.

Suy ra $\widehat{ABC}=\widehat{ACB}$.

Vậy các câu a), c), d) đúng.

Câu b) chưa đúng vì ta chưa đủ dữ kiện để tam giác ABC đều, do ta chỉ có AB = AC, và độ dài đoạn thẳng BC bất kì.

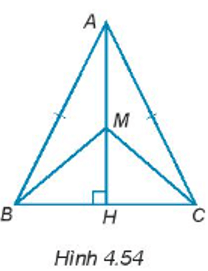
Bài 4.50 trang 70 sách bài tập Toán lớp 7 Tập 1: Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường thẳng AH sao cho M không trùng với A (H.4.54).

Chứng minh rằng: $\widehat{MBA}=\widehat{MCA}$.

Lời giải:

Xét tam giác vuông ABH và tam giác vuông ACH có:

AB = AC (∆ABC cân tại đỉnh A)

AH: cạnh chung

Do đó, ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông).

Suy ra $\widehat{BAH}=\widehat{CAH}$, hay $\widehat{BAM}=\widehat{CAM}$.

Xét tam giác ABM và ACM có:

AB = AC (∆ABC cân tại đỉnh A)

$\widehat{BAM}=\widehat{CAM}$

AM: cạnh chung

Do đó, ∆ABM = ∆ACM (c – g – c).

Suy ra $\widehat{MBA}=\widehat{MCA}$.

Lời giải sách bài tập Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Kết nối tri thức hay khác:

• Giải SBT Toán 7 trang 68 Tập 1

• Giải SBT Toán 7 trang 69 Tập 1