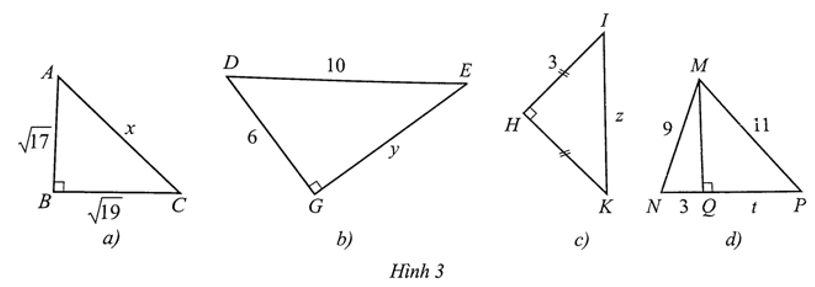
Tính độ dài x, y, z, t ở các hình 3a, 3b, 3c, 3d

Giải SBT Toán 8 Bài 1: Định lí Pythagore - Cánh diều

Bài 1 trang 87 SBT Toán 8 Tập 1: Tính độ dài x, y, z, t ở các hình 3a, 3b, 3c, 3d (độ dài ở các hình là cùng đơn vị đo):

Lời giải:

a) Do tam giác ABC vuông tại B nên theo định lý Pythagore, ta có:

AC² = AB² + BC²

Suy ra $A C^{2} = {(\sqrt{17})}^{2} + {(\sqrt{19})}^{2} = 17 + 19 = 36$ .

Do đó $A C = \sqrt{36} = 6$ hay x = 6.

b) Do tam giác DGE vuông tại G nên theo định lý Pythagore, ta có:

DE² = DG² + GE²

Suy ra GE² = DE² ‒ DG² = 10² ‒ 6² = 100 – 36 = 64

Do đó $G E = \sqrt{64} = 8$ hay y = 8.

c) Xét tam giác IHK cân tại H có HK = HI = 3.

Do tam giác IHK vuông tại H nên theo định lý Pythagore, ta có:

IK² = IH² + HK² = 3² + 3² = 18

Suy ra $I K = \sqrt{18}$ hay $z = \sqrt{18}$ .

d) Do tam giác MNQ vuông tại Q nên theo định lý Pythagore, ta có:

MN² = MQ² + NQ²

Suy ra MQ² = MN² ‒ NQ² = 9² ‒ 3² = 81 – 9 = 72

Do tam giác MQP vuông tại Q nên theo định lý Pythagore, ta có:

MP² = MQ² + QP²

Suy ra QP² = MP² ‒ MQ² = 11² ‒ 72 = 121 – 72 = 49

Do đó $Q P = \sqrt{49} = 7$ hay t = 7.

Lời giải SBT Toán 8 Bài 1: Định lí Pythagore hay khác: