Cho tam giác đều ABC có độ dài cạnh là 6 cm

---

Giải SBT Toán 8 Bài 2: Tứ giác - Cánh diều

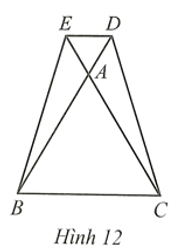
Bài 15 trang 92 SBT Toán 8 Tập 1: Cho tam giác đều ABC có độ dài cạnh là 6 cm. Trên tia BA, CA lần lượt lấy điểm D, E sao cho AD = AE = 2 cm (Hình 12).

a) Tứ giác BCDE là hình gì? Vì sao?

b*) Tính độ dài đoạn thẳng CD (làm tròn kết quả đến hàng phần mười của centimét).

Lời giải:

a) Tam giác đều ABC có AB = BC = AC = 6 cm; $\widehat{BAC}=\widehat{CBA}=\widehat{ACB}=60°$.

Ta có: $\widehat{DAE}=\widehat{BAC}$ (hai góc đối đỉnh) nên $\widehat{DAE}=60°$.

Tam giác ADE có AD = AE và $\widehat{DAE}=60°$ nên ∆ADE là tam giác đều.

Suy ra $\widehat{ADE}=60°$. Do đó $\widehat{CBA}=\widehat{ADE}$ (vì cùng bằng 60°).

Mà $\widehat{CBA}$ và $\widehat{ADE}$ nằm ở vị trí so le trong, suy ra BC // DE.

Ta có: AB = AC và AD = AE, mà BD = AB + AD, CE = AC + AE

Suy ra BD = CE.

Tứ giác BCDE có BC // DE và BD = CE nên BCDE là hình thang cân.

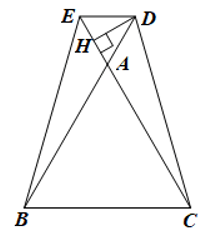
b*) Kẻ DH vuông góc với CE tại H.

Xét ∆ADH vuông tại H và ∆EDH vuông tại H có:

ED = AD (chứng minh câu a), cạnh DH chung

Do đó ∆ADH = ∆EDH (cạnh huyền – cạnh góc vuông).

Suy ra AH = EH (hai cạnh tương ứng)

Hay H là trung điểm của AE nên $AH=EH=\frac{AE}{2}=\frac{2}{2}=1 \left(\text{cm}\right)$.

Áp dụng định lý Pythagore cho tam giác ADH vuông tại H, ta có: AD² = AH² + DH².

Suy ra DH² = AD² ‒ AH² = 2² ‒ 1² = 3.

Ta có: CH = AC + AH = 6 + 1 = 7 cm.

Áp dụng định lý Pythagore cho tam giác CDH vuông tại H, ta có: CD² = CH² + DH².

Suy ra CD² = 7² + 3 = 49 + 3 = 52.

Vậy $CD=\sqrt{52}\approx \mathrm{7,2} \left(\text{cm}\right)$.

Lời giải SBT Toán 8 Bài 2: Tứ giác hay khác:

• Bài 11 trang 92 SBT Toán 8 Tập 1: Cho tứ giác ABCD có $\widehat{C}=\widehat{D}$ và AD = BC. Chứng minh tứ giác ABCD ....

• Bài 12 trang 92 SBT Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, AB < CD, hai đường chéo AC ....

• Bài 13 trang 92 SBT Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, AB = 3 cm, CD = 6 cm, AD = 2,5 cm ....

• Bài 14 trang 92 SBT Toán 8 Tập 1: Cho tam giác ABC cân tại A. Lấy điểm M, N lần lượt trên cạnh AB, AC ....