Cho tam giác ABC có AB = AC = 3 cm Từ điểm M thuộc cạnh BC
Giải SBT Toán 8 Bài 4: Hình bình hành - Cánh diều
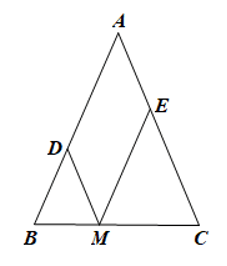
Bài 16 trang 94 SBT Toán 8 Tập 1: Cho tam giác ABC có AB = AC = 3 cm. Từ điểm M thuộc cạnh BC, kẻ MD song song với AC và ME song song với AB (điểm D, E lần lượt thuộc cạnh AB, AC). Tính chu vi của tứ giác ADME.
Lời giải:
Tứ giác ADME có MD // AE, ME // AD nên ADME là hình bình hành.
Suy ra AD = ME và AE = DM.
Do đó chu vi hình bình hành ADME là:
AD + DM + ME + EA = 2(AE + ME).
Do AB = AC nên tam giác ABC cân tại A. Suy ra .
Mà (hai góc đồng vị do ME // AB), suy ra .
Do đó, tam giác ECM cân tại E. Suy ra ME = CE.
Vậy chu vi của hình bình hành ADME là:
2(AE + ME) = 2(AE + CE) = 2AC = 6 cm.
Lời giải SBT Toán 8 Bài 4: Hình bình hành hay khác: