Cho tam giác nhọn ABC có ba đường cao AM, BN, CP cắt nhau tại
Giải SBT Toán 8 Bài 4: Hình bình hành - Cánh diều
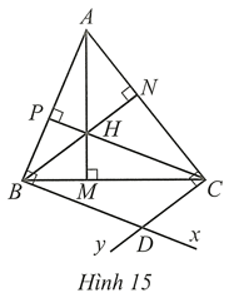
Bài 19 trang 95 SBT Toán 8 Tập 1: Cho tam giác nhọn ABC có ba đường cao AM, BN, CP cắt nhau tại H. Qua B kẻ tia Bx vuông góc với AB. Qua C kẻ tia Cy vuông góc với AC. Gọi D là giao điểm của Bx và Cy (Hình 15).
a) Chứng minh tứ giác BDCH là hình bình hành.
b*) Tam giác ABC có điều kiện gì thì ba điểm A, D, H thẳng hàng?
c) Tìm mối liên hệ giữa góc A và góc D của tứ giác ABDC.
d) Giả sử H là trung điểm của AM. Chứng minh diện tích của tam giác ABC bằng diện tích của tứ giác BHCD.
Lời giải:
a) Do AM, BN, CP là đường cao của ∆ABC nên AM ⊥ BC, BN ⊥ AC, CP ⊥ AB
Do CP ⊥ AB, BD ⊥ AB nên CP // BD.
Do BN ⊥ AC, CD ⊥ AC nên BN // CD
Tứ giác BDCH có BD // CH, BH // CD nên BDCH là hình bình hành.
b*) Để ba điểm A, D, H thẳng hàng thì M phải thuộc DH.
Mà M thuộc BC, suy ra M là giao điểm của BC và DH.
Do BDCH là hình bình hành nên hai đường chéo BC và DH cắt nhau tại trung điểm mỗi đường. Suy ra M là trung điểm BC. Suy ra MB = MC
Xét ∆ABM và ∆ACM có:
MB = MC, , cạnh AM chung
Do đó ∆ABM = ∆ACM (c.g.c). Suy ra AB = AC (hai cạnh tương ứng)
Dễ thấy, nếu tam giác ABC có AB = AC thì ba điểm A, D, H thẳng hàng.
Vậy tam giác ABC cân tại A thì ba điểm A, D, H thẳng hàng.
c) Xét tứ giác ABDC, ta có: .
Mà , suy ra .
Vậy góc A và góc D của tứ giác ABDC là hai góc bù nhau.
d) Do H là trung điểm của AM nên .
Ta có diện tích tam giác ABC bằng: .
Xét ∆BCH và ∆CBD có:
BH = CD, BD = HC (do BDCH là hình bình hành), cạnh BC chung
Do đó ∆BCH = ∆CBD (c.c.c)
Suy ra S∆BCH = S∆CBD
Nên diện tích tứ giác BHCD bằng 2 lần diện tích tam giác BCH.
Khi đó, diện tích tứ giác BHCD bằng: .
Vậy diện tích của tam giác ABC bằng diện tích của tứ giác BHCD.
Lời giải SBT Toán 8 Bài 4: Hình bình hành hay khác: