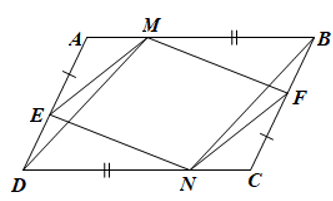
Cho hình bình hành ABCD Trên cạnh AD, BC lần lượt lấy điểm
Giải SBT Toán 8 Bài 4: Hình bình hành - Cánh diều
Bài 18 trang 95 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Trên cạnh AD, BC lần lượt lấy điểm E, F sao cho AE = CF. Trên cạnh AB, CD lần lượt lấy điểm M, N sao cho BM = DN. Chứng minh:
a) Tứ giác ENFM là hình bình hành;
b) Bốn đường thẳng AC, BD, EF, MN cùng đi qua một điểm.
Lời giải:
a) Do ABCD là hình bình hành nên AD = BC và AB = CD; và .
Mà AE = CF, AE + ED = AD, BF + CF = BC
Suy ra DE = BF.
Tương tự, ta cũng có AM = CN.
Xét ∆AEM và ∆CFN có:
AM = CN, , AE = CF
Do đó ∆AEM và ∆CFN (c.g.c). Suy ra EM = FN (hai cạnh tương ứng)
Xét ∆BFM và ∆DEN có:
BF = DE, , BM = DN
Do đó ∆BFM = ∆DEN (c.g.c). Suy ra FM = EN.
Tứ giác EMFN có EM = FN và FM = EN nên EMFN là hình bình hành.
b) Tứ giác BMDN có BM = DN và BM // DN nên BMDN là hình bình hành.
Do ABCD, EMFN, BMDN đều là hình bình hành nên các đường chéo của mỗi hình bình hành cắt nhau tại trung điểm của mỗi đường.
Vậy AC, BD, EF, MN cùng đi qua trung điểm của mỗi đường.
Lời giải SBT Toán 8 Bài 4: Hình bình hành hay khác: