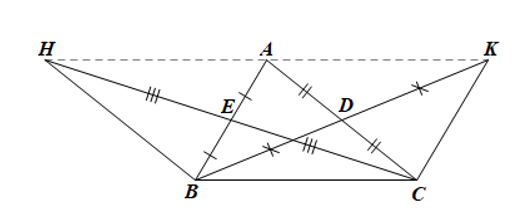
Cho tam giác ABC có các đường trung tuyến BD và CE
Giải SBT Toán 8 Bài 4: Hình bình hành - Cánh diều
Bài 17 trang 94 SBT Toán 8 Tập 1: Cho tam giác ABC có các đường trung tuyến BD và CE. Lấy các điểm H, K sao cho E là trung điểm của CH, D là trung điểm của BK. Chứng minh:
a) Các tứ giác AHBC, AKCB là hình bình hành;
b) A là trung điểm của HK.
Lời giải:
a) Do BD và CE là trung tuyến của ∆ABC
Suy ra, E là trung điểm AB và D là trung điểm AC.
Tứ giác AHBC có E là trung điểm AB và CH nên AHBC là hình bình hành.
Tứ giác ABCK có D là trung điểm AC và BK nên ABCK là hình bình hành.
b) Do AHBC là hình bình hành nên AH // BC, AH = BC.
Tương tự, AKCB là hình bình hành nên AK // BC, AK = BC.
Suy ra ba điểm H, A, K thẳng hàng và AH = AK.
Vậy A là trung điểm của HK.
Lời giải SBT Toán 8 Bài 4: Hình bình hành hay khác: