Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O
Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.
Giải SBT Toán 8 Bài 4: Hình bình hành – Hình thoi - Chân trời sáng tạo
Bài 1 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.
Lời giải:
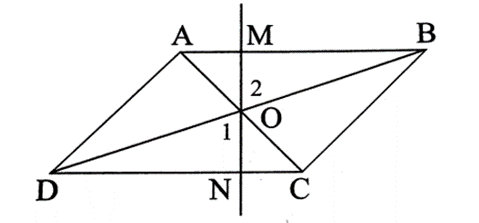
Do ABCD là hình bình hành nên AB // CD, suy ra (hai góc so le trong);
OB = OD (tính chất đường chéo của hình bình hành);
Xét ∆DON và ∆BOM ta có:
;
OD = OB;
(hai góc đối đỉnh).
Suy ra ∆DON = ∆BOM (g.c.g).
Do đó OM = ON (hai cạnh tương ứng)
Vậy O là trung điểm của MN.
Lời giải SBT Toán 8 Bài 4: Hình bình hành – Hình thoi hay khác:
Bài 2 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD ...
Bài 3 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho AM = CN ...
Bài 4 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho ...
Bài 5 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD có AD = 2AB. Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N ...
Bài 6 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Vẽ hình bình hành AECF (E ∈ AB, F ∈ CD). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy ...
Bài 7 trang 65 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành ...
Bài 8 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD ...

