Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O

Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.

Giải SBT Toán 8 Bài 4: Hình bình hành – Hình thoi - Chân trời sáng tạo

Bài 8 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.

Lời giải:

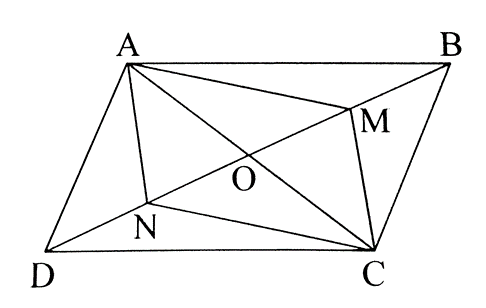
Tứ giác ABCD là hình bình hành nên OA = OC và OB = OD.

Ta có: $ON=\frac{1}{2}OD$ (N là trung điểm của OD); $OM=\frac{1}{2}OB$ (M là trung điểm của OB); OB = OD (chứng minh trên).

Suy ra OM = ON.

Xét tứ giác AMCN ta có: OM = ON, OA = OC (chứng minh trên)

Do đó, tứ giác AMCN là hình bình hành.

Lời giải SBT Toán 8 Bài 4: Hình bình hành – Hình thoi hay khác:

• Bài 1 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N ...

• Bài 2 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD ...

• Bài 3 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho AM = CN ...

• Bài 4 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho $BM=DN=\frac{1}{3}BD$ ...

• Bài 5 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD có AD = 2AB. Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N ...

• Bài 6 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Vẽ hình bình hành AECF (E ∈ AB, F ∈ CD). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy ...

• Bài 7 trang 65 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành ...