Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC
Giải SBT Toán 8 Bài 5: Hình chữ nhật – Hình vuông - Chân trời sáng tạo
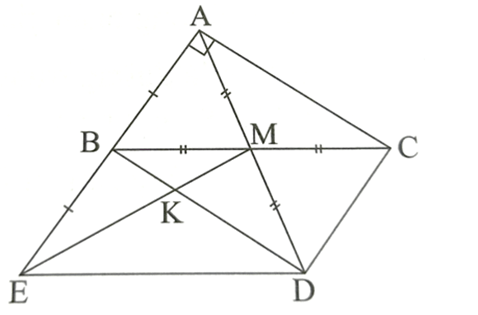
Bài 1 trang 71 sách bài tập Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC.
Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b) Gọi E là điểm đối xứng của A qua B. Chứng minh tứ giác BEDC là hình bình hành.
c) EM cắt BD tại K. Chứng minh EK = 2KM.
Lời giải:
a) Xét tứ giác ABDC có: AM = MD (M ∈ AD); BM = MC (M ∈ BC).
Suy ra tứ giác ABDC là hình bình hành.
Ta lại có (do ∆ABC vuông tại A).
Do đó, tứ giác ABDC là hình chữ nhật.
b) Tứ giác ABDC là hình chữ nhật (theo câu a), suy ra AB = CD và AB // CD.
Do E đối xứng với A qua B nên B, A, E thẳng hàng và AB = BE.
Vì AB // CD nên BE // CD.
Vì AB = CD và AB = BE nên CD = BE.
Xét tứ giác BEDC có BE // CD và BE = CD nên là hình bình hành.
c) ∆AED có hai đường trung tuyến EM và DB cắt nhau tại K, nên K là trọng tâm của tam giác AED.
Suy ra và nên EK = 2KM.
Lời giải SBT Toán 8 Bài 5: Hình chữ nhật – Hình vuông hay khác: