Cho tam giác DEF vuông tại D (DE > DF), DM là đường trung tuyến (M ∈ EF)
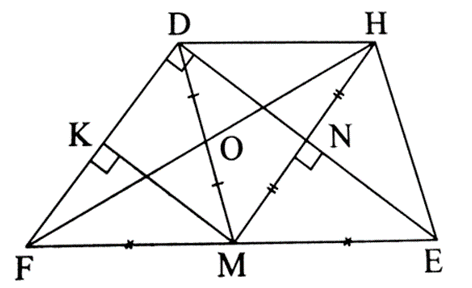
Cho tam giác DEF vuông tại D (DE > DF), DM là đường trung tuyến (M ∈ EF). Gọi MN là đường vuông góc kẻ từ M đến DE (N ∈ DE), MK là đường vuông góc kẻ từ M đến DF (K ∈ DF), H là điểm đối xứng với M qua N.
Giải SBT Toán 8 Bài 5: Hình chữ nhật – Hình vuông - Chân trời sáng tạo
Bài 2 trang 71 sách bài tập Toán 8 Tập 1: Cho tam giác DEF vuông tại D (DE > DF), DM là đường trung tuyến (M ∈ EF). Gọi MN là đường vuông góc kẻ từ M đến DE (N ∈ DE), MK là đường vuông góc kẻ từ M đến DF (K ∈ DF), H là điểm đối xứng với M qua N.
a) Tứ giác DKMN là hình gì Vì sao?
b) Gọi O là trung điểm của DM. Chứng minh ba điểm H, O , F thẳng hàng.
c) Tam giác DEF cần thêm điều kiện gì để tứ giác DKMN là hình vuông?
Lời giải:
a) Do MN ⊥ DE tại N, MK ⊥ DF tại K nên và
Tứ giác DKMN có nên DKMN là hình chữ nhật.
b) ∆DEF vuông tại D và DM là đường trung tuyến ứng với cạnh huyền nên
.
Suy ra ∆MDE cân tại M.
Ta lại có MN ⊥ DE tại N, suy ra đường cao MN cũng đồng thời là đường trung tuyến của ∆MDE, suy ra .
Tứ giác DHEM có: ND = NE và NH = NM (do H là điểm đối xứng với M qua N).
Suy ra DHEM là hình bình hành.
Do đó DH // ME và DH = ME.
Mà M là trung điểm EF nên ME = MF
Khi đó DH // MF và DH = MF nên tứ giác DHMF là hình bình hành.
Hơn nữa, O là trung điểm của DM, suy ra O cũng là trung điểm của HF.
Vậy H, O, F thẳng hàng.
c) Hình chữ nhật DKMN là hình vuông khi DM là đường phân giác của , hay DM là đường phân giác của .
Khi đó DM là đường trung tuyến và cũng là đường phân giác xuất phát từ D của ∆DEF
Do đó ∆DEF cân tại D
Suy ra ∆DEF vuông cân tại D.
Vậy ∆DEF vuông cân tại D thì DKMN là hình vuông.
Lời giải SBT Toán 8 Bài 5: Hình chữ nhật – Hình vuông hay khác: