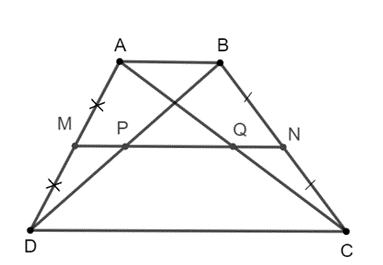
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AD, BC
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AD, BC, BD, AC. Chứng minh bốn điểm M, N, P, Q thẳng hàng.
Giải sách bài tập Toán 8 Bài 2: Đường trung bình của tam giác - Chân trời sáng tạo
Bài 4 trang 45 sách bài tập Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AD, BC, BD, AC. Chứng minh bốn điểm M, N, P, Q thẳng hàng.
Lời giải:
• Xét ∆ABD, ta có MA = MD và PB = PD nên MP là đường trung bình của ∆ABD.
Suy ra MP //AB mà AB // CD nên MP // CD.
• Xét ∆ADC, ta có MA = MD và QA = QC nên MQ là đường trung bình của ∆ADC.
Suy ra MQ // CD.
• Xét ∆BCD, ta có PB = PD và NB = NC nên BN là đường trung bình của ∆BCD.
Suy ra PN // CD.
Qua điểm M ∉ CD có MP // CD và MQ // CD, suy ra M, P, Q thẳng hàng. (1)
Qua điểm P ∉ CD có MP // CD và PN // CD, suy ra M, P, N thẳng hàng. (2)
Từ (1) và (2) suy ra bốn điểm M, N, P, Q thẳng hàng.
Lời giải SBT Toán 8 Bài 2: Đường trung bình của tam giác hay khác: