Cho tam giác ABC có AM là đường trung tuyến (M ∈ BC). Lấy điểm E thuộc AM

Cho tam giác ABC có AM là đường trung tuyến (M ∈ BC). Lấy điểm E thuộc AM sao cho AE = 3EM. Tia BE cắt AC tại N. Tính tỉ số .

Giải sách bài tập Toán 8 Bài 1: Định lí Thalès trong tam giác - Chân trời sáng tạo

Bài 5 trang 42 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có AM là đường trung tuyến (M ∈ BC). Lấy điểm E thuộc AM sao cho AE = 3EM. Tia BE cắt AC tại N. Tính tỉ số $\frac{AN}{NC}$.

Lời giải:

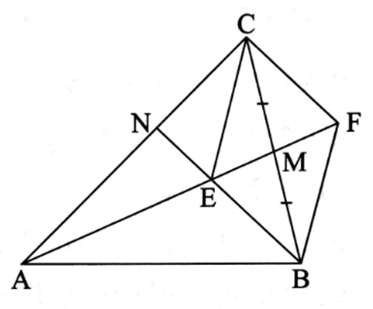
Lấy điểm F trên tia AM sao cho M là trung điểm của EF.

Tứ giác MEFC có hai hai đường chéo BC và EF cắt nhau tại trung điểm của mỗi đường nên tứ giác MEFC là hình bình hành.

Suy ra CF // BE và CF // EN.

Ta có AE = 3EM và ME = MF (vì M là trung điểm của EF).

Khi đó, $\frac{AE}{EF}=\frac{3}{2}$.

Xét ∆ACF có CF // EN nên theo định lí Thalès, ta có: $\frac{AN}{NC}=\frac{AE}{EF}=\frac{3}{2}$.

Vậy $\frac{AN}{NC}=\frac{3}{2}$.

Lời giải SBT Toán 8 Bài 1: Định lí Thalès trong tam giác hay khác:

• Bài 1 trang 41 sách bài tập Toán 8 Tập 2: Trên một đường thẳng, đặt ba đoạn thẳng liên tiếp AB = BC = CD ...

• Bài 2 trang 42 sách bài tập Toán 8 Tập 2: Cho đoạn thẳng AB có độ dài bằng 10 cm. Lấy điểm C thuộc đoạn thẳng AB sao cho $\frac{CA}{CB}=\frac{3}{2}$. Lấy D thuộc tia đối của tia BA sao cho $\frac{DA}{DB}=\frac{3}{2}$ ...

• Bài 3 trang 42 sách bài tập Toán 8 Tập 2: Trong Hình 10, cho biết QR // NP và MQ = 10 cm, QN = 5 cm, RP = 6 cm. Tính độ dài MR ...

• Bài 4 trang 42 sách bài tập Toán 8 Tập 2: Tính các độ dài x, y trong Hình 11 ...

• Bài 6 trang 42 sách bài tập Toán 8 Tập 2: Cho tam giác ABC và điểm D trên cạnh BC sao cho $\frac{BD}{BC}=\frac{3}{4}$, điểm E trên đoạn AD sao cho $\frac{AE}{AD}=\frac{1}{3}$ ...

• Bài 7 trang 42 sách bài tập Toán 8 Tập 2: Cho tam giác ABC và điểm M trên cạnh AB sao cho $\frac{AM}{MB}=\frac{3}{2}$. Kẻ MN // BC (N ∈ AC). Cho biết BC = 6 cm, tính độ dài MN ...

• Bài 8 trang 42 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A và MN // BC (M ∈ AB; N ∈ AC). Cho biết AB = 9 cm, AM = 3 cm, AN = 4 cm. Tính độ dài NC, MN, BC ...