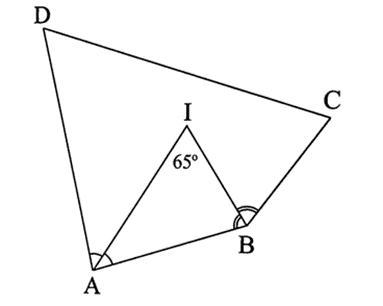
Cho tứ giác ABCD có góc C + góc D = 10°

Cho tứ giác .

Giải SBT Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

Bài 5 trang 57 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD có $\hat{C}-\hat{D}=10°$. Các tia phân giác của góc A và góc B cắt nhau tại I. Biết $\widehat{AIB}=65°$. Tính số đo góc C và góc D.

Lời giải:

Xét ∆AIB, ta có: $\widehat{AIB}+\widehat{IAB}+\widehat{IBA}=180°$

Mà $\widehat{AIB}=65°$ suy ra $\widehat{IAB}+\widehat{IBA}=180°-65°=115°$.

Do AI, BI lần lượt là tia phân giác của $\widehat{DAB},\widehat{ABC}$ nên ta có:

$\widehat{DAB}=2\widehat{IAB},\widehat{ABC}=2\widehat{IBA}$

Do đó $\hat{A}+\hat{B}=\widehat{DAB}+\widehat{ABC}=2.\left(\widehat{IAB}+\widehat{IBA}\right)=2.115°=230°$.

Xét tứ giác $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

Suy ra $\hat{C}+\hat{D}=360°-\left(\hat{A}+\hat{B}\right)=360°-230°=130°$.

Mặt khác $\hat{C}-\hat{D}=10°$nên $\hat{C}=10°+\hat{D}$

Thay $\hat{C}=10°+\hat{D}$ vào $\hat{C}+\hat{D}=130°$ ta có:

$10°+\hat{D}+\hat{D}=130°$

Suy ra, $\hat{D}=\frac{130°-10°}{2}=60°$.

Do đó $\hat{C}=60°+10°=70°$.

Lời giải SBT Toán 8 Bài 2: Tứ giác hay khác:

• Bài 1 trang 56 sách bài tập Toán 8 Tập 1: Tìm tứ giác lồi trong các hình sau ...

• Bài 2 trang 57 sách bài tập Toán 8 Tập 1: Tìm số đo x trong các tứ giác sau ...

• Bài 3 trang 57 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD như Hình 12. Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD ...

• Bài 4 trang 57 sách bài tập Toán 8 Tập 1: Bạn Hùng muốn làm một cái diều có dạng hình tứ giác KITE như Hình 13 ...

• Bài 6 trang 57 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD có AB = AD, CB = CD, $\hat{C}=65°,\hat{A}=115°$ ...

• Bài 7 trang 57 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết BC = 15 cm, CD = 24 cm và AD = 20 cm ...

• Bài 8 trang 57 sách bài tập Toán 8 Tập 1: Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi của tứ giác đó ...