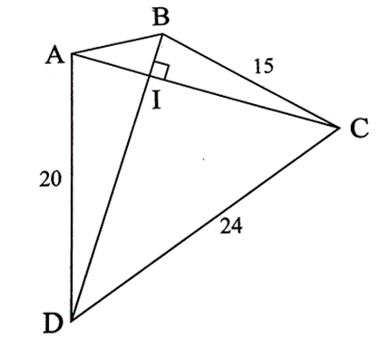
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I

Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết BC = 15 cm, CD = 24 cm và AD = 20 cm. Tính độ dài AB.

Giải SBT Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

Bài 7 trang 57 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết BC = 15 cm, CD = 24 cm và AD = 20 cm. Tính độ dài AB.

Lời giải:

Áp dụng định lí Pythagore vào bốn tam giác AIB, BIC, CID, DIA vuông tại I, ta có:

AB² = IA² + IB²

BC² = IB² + IC²

CD² = IC² + ID²

AD² = IA² + ID²

Nên AB² + CD² = IA² + IB² + IC² + ID²

Hay AB² + CD² = (IB² + IC²) + (IA² + ID²)

AB² + CD² = BC² + AD²

AB² + 24² = 15² + 20²

AB² = 225 + 400 – 576 = 49

Suy ra $AB=\sqrt{49}=7$ (cm).

Lời giải SBT Toán 8 Bài 2: Tứ giác hay khác:

• Bài 1 trang 56 sách bài tập Toán 8 Tập 1: Tìm tứ giác lồi trong các hình sau ...

• Bài 2 trang 57 sách bài tập Toán 8 Tập 1: Tìm số đo x trong các tứ giác sau ...

• Bài 3 trang 57 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD như Hình 12. Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD ...

• Bài 4 trang 57 sách bài tập Toán 8 Tập 1: Bạn Hùng muốn làm một cái diều có dạng hình tứ giác KITE như Hình 13 ...

• Bài 5 trang 57 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD có $\hat{C}-\hat{D}=10°$. Các tia phân giác của góc A và góc B cắt nhau tại I ...

• Bài 6 trang 57 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD có AB = AD, CB = CD, $\hat{C}=65°,\hat{A}=115°$ ...

• Bài 8 trang 57 sách bài tập Toán 8 Tập 1: Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi của tứ giác đó ...