Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M

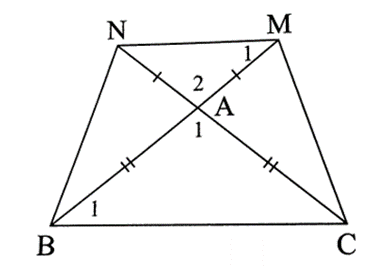
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia AC lấy điểm N sao cho AM = AN. Chứng minh tứ giác MNBC là hình thang cân.

Giải SBT Toán 8 Bài 3: Hình thang – Hình thang cân - Chân trời sáng tạo

Bài 5 trang 60 sách bài tập Toán 8 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia AC lấy điểm N sao cho AM = AN. Chứng minh tứ giác MNBC là hình thang cân.

Lời giải:

Xét ∆AMN có AM = AN (giả thiết).

Do đó ∆AMN cân tại A, suy ra $\widehat{M_1}=\frac{180°-\widehat{A_2}}{2}$.

Vì ∆ABC cân tại A nên $\widehat{B_1}=\frac{180°-\widehat{A_1}}{2}$.

Lại có $\widehat{A_1}=\widehat{A_2}$ (hai góc đối đỉnh) nên $\widehat{B_1}=\widehat{M_1}$.

Mà hai góc này ở vị trí so le trong nên MN // BC.

Vậy tứ giác MNBC là hình thang.(1)

Mặt khác, AB = AC; AM = AN.

Suy ra AB + AM = AC + AN, do đó MB = NC (2)

Từ (1) và (2) suy ra MNBC là hình thang cân.

Lời giải SBT Toán 8 Bài 3: Hình thang – Hình thang cân hay khác:

• Bài 1 trang 60 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh tứ giác ABCD là hình thang ...

• Bài 2 trang 60 sách bài tập Toán 8 Tập 1: Tứ giác ABCD có $\hat{A}+\hat{D}=\hat{B}+\hat{C}$. Chứng minh tứ giác ABCD là hình thang ...

• Bài 3 trang 60 sách bài tập Toán 8 Tập 1: Cho tam giác ABC vuông cân tại A. Vẽ ra phía ngoài của tam giác ABC một tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? ...

• Bài 4 trang 60 sách bài tập Toán 8 Tập 1: Hình thang ABCD (AB // CD) có $\widehat{ACD}=\widehat{BDC}$. Chứng minh tứ giác ABCD là hình thang cân ...

• Bài 6 trang 60 sách bài tập Toán 8 Tập 1: Cho tam giác ABC cân tại A, có hai đường cao là BE và CD (D ∈ AB, E ∈ AC). Chứng minh tứ giác BDEC là hình thang cân ...