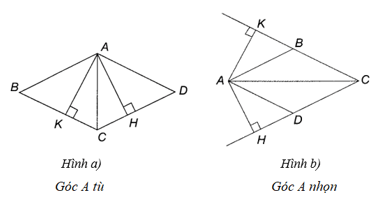
Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi
Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi.
Giải sách bài tập Toán 8 Bài 14: Hình thoi và hình vuông - Kết nối tri thức
Bài 3.23 trang 42 sách bài tập Toán 8 Tập 1: Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi.
Lời giải:
Xét hình bình hành ABCD có đường cao AH (H thuộc đường thẳng CD), và đường cao AK (K thuộc đường thẳng BC), AH = AK.
Xét DACH vuông tại H và DACK vuông tại K có:
Cạnh AC chung, AH = AK
Do đó ∆ACH = ∆ACK (cạnh huyền – một cạnh góc vuông)
Suy ra (hai góc tương ứng)
Nên CA là tia phân giác của .
Hình bình hành ABCD có CA là phân giác nên là hình thoi.
Lời giải SBT Toán 8 Bài 14: Hình thoi và hình vuông hay khác: