Trên mặt phẳng toạ độ Oxy cho M(–4; 0), N(4; 0) và P(3; 3). Phép quay ngược chiều α độ tâm O biến điểm M thành điểm N
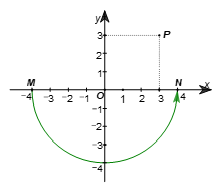
Trên mặt phẳng toạ độ Oxy cho M(–4; 0), N(4; 0) và P(3; 3).
Giải SBT Toán 9 Bài 2: Phép quay - Cánh diều
Bài 13 trang 111 SBT Toán 9 Tập 2: Trên mặt phẳng toạ độ Oxy cho M(–4; 0), N(4; 0) và P(3; 3).
a) Phép quay ngược chiều α° tâm O biến điểm M thành điểm N. Tìm α.
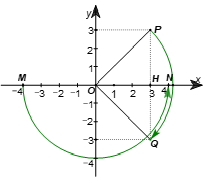
b) Qua phép quay thuận chiều 90° tâm O, điểm P biến thành điểm nào?
Lời giải:
a)
Ta có: M(–4; 0), N(4; 0) suy ra OM = |–4| = 4; ON = |4| = 4.
Do đó OM = OM. (1)
Ta cũng suy ra được điểm M và điểm N cùng nằm trên trục Ox, đối xứng với nhau qua điểm O, khi đó
Do đó, tia OM quay đến tia ON theo chiều ngược kim đồng hồ tạo thành một cung có số đo bằng 180°. (2)
Từ (1) và (2), ta có phép quay ngược chiều 180° tâm O biến điểm M thành điểm N.
Vậy α = 180.
b)
Gọi H là hình chiếu của điểm P trên Ox.
Do P(3; 3) nên H(3; 0). Suy ra OH = 3 và PH = 3.
Do đó ∆OPH vuông cân tại H, nên
Gọi Q là điểm đối xứng với P(3; 3) qua Ox. Khi đó Q(3; –3).
Ta cũng chứng minh được
Khi đó,
Mặt khác, P và Q đối xứng với nhau qua Ox hay OH là trung trực của PQ, nên OP = OQ. Do đó tia OP quay đến tia OQ theo chiều kim đồng hồ tạo thành một cung có số đo bằng 90°.
Vậy phép quay thuận chiều 90° tâm O điểm P(3; 3) biến thành điểm Q(3; – 3).
Lời giải SBT Toán 9 Bài 2: Phép quay hay khác: