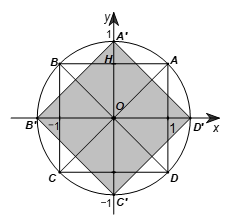
Trên mặt phẳng tọa độ Oxy, cho hình vuông ABCD với A(1; 1), B(–1; 1), C(–1; –1), D(1; –1)
Trên mặt phẳng tọa độ Oxy, cho hình vuông ABCD với A(1; 1), B(–1; 1), C(–1; –1), D(1; –1). Phép quay ngược chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính diện tích tứ giác A’B’C’D’.
Giải SBT Toán 9 Bài 2: Phép quay - Cánh diều
Bài 18 trang 112 SBT Toán 9 Tập 2: Trên mặt phẳng tọa độ Oxy, cho hình vuông ABCD với A(1; 1), B(–1; 1), C(–1; –1), D(1; –1). Phép quay ngược chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính diện tích tứ giác A’B’C’D’.
Lời giải:
Gọi H là hình chiếu của A trên Oy.
Ta có A(1; 1) nên suy ra AH = OH = 1.
Do đó ∆OAH vuông cân tại H nên
Xét ∆OAH vuông tại H, ta có: OA2 = OH2 + AH2 (định lí Pythagore)
Suy ra
Tương tự, ta sẽ có
Mặt khác, do ABCD là hình vuông nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường, do đó O là tâm của hình vuông.
Do đó, phép quay ngược chiều 45° tâm O biến điểm A thành các điểm A’ nằm trên tia Oy sao cho tức là
Tương tự, ta chứng minh được, phép quay ngược chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm
Suy ra tứ giác A’B’C’D’ là hình vuông với hai đường chéo là A’C’ và B’D’, nên diện tích tứ giác A’B’C’D’ là:
(đơn vị diện tích).
Lời giải SBT Toán 9 Bài 2: Phép quay hay khác: