Môt người đứng chào cờ (ở vị trí A) cách cột cờ (ở vị trí C) với AC = 20 m

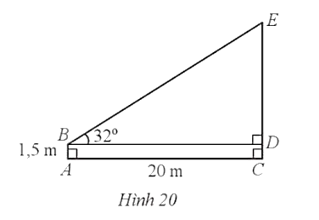
Môt người đứng chào cờ (ở vị trí A) cách cột cờ (ở vị trí C) với AC = 20 m. Người đó đặt mắt tại vị trí B cách mặt đất một khoảng là AB = 1,5 m. Người đó nhìn lên đỉnh cột cờ (ở vị trí E) theo phương BE tạo với phương nằm ngang BD một góc là (Hình 20). Tính chiều cao của cột cờ (làm tròn kết quả đến hàng đơn vị của mét).

Giải SBT Toán 9 Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn - Cánh diều

Bài 20 trang 88 SBT Toán 9 Tập 1: Môt người đứng chào cờ (ở vị trí A) cách cột cờ (ở vị trí C) với AC = 20 m. Người đó đặt mắt tại vị trí B cách mặt đất một khoảng là AB = 1,5 m. Người đó nhìn lên đỉnh cột cờ (ở vị trí E) theo phương BE tạo với phương nằm ngang BD một góc là $\widehat{EBD}=32°$ (Hình 20). Tính chiều cao của cột cờ (làm tròn kết quả đến hàng đơn vị của mét).

Lời giải:

Do $\widehat{BAC}=\widehat{ACD}=\widehat{CDB}=90°$ nên ABDC là hình chữ nhật.

Suy ra CD = AB = 1,5 m và BD = AC = 20 m.

Vì tam giác BDE vuông tại D nên $DE=BD\cdot \tan \widehat{EBD}=20\cdot \tan 32°.$

Khi đó: CE = CD + DE = 1,5 + 20.tan 32° ≈ 14 (m).

Vậy chiều cao của cột cờ khoảng 14 mét.

Lời giải SBT Toán 9 Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn hay khác:

• Bài 18 trang 87 SBT Toán 9 Tập 1: Tính chiều cao của cột cờ (làm tròn kết quả đến hàng phần trăm của mét), biết bóng của cột cờ được chiếu bởi ánh sáng Mặt Trời xuống mặt đất ...

• Bài 19 trang 87 SBT Toán 9 Tập 1: Một khối u (ở vị trí A ) của một bệnh nhân cách da mặt 5,7 cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô...

• Bài 21 trang 88 SBT Toán 9 Tập 1: Bạn Hoà vẽ mặt cắt đứng phần mái của một ngôi nhà có dạng tam giác cân ABC (mái hai dốc). Biết rằng góc tạo bởi phần mái nhà ....

• Bài 22 trang 88 SBT Toán 9 Tập 1: Trên mặt biển, khi khoảng cách từ ca nô đến chân tháp hải đăng là AB = 300 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C ....

• Bài 23 trang 88 SBT Toán 9 Tập 1: Một chiếc thuyền đi với tốc độ 20 km/h theo hướng Đông trong 1 giờ 30 phút từ vị trí P đến vị trí A. Sau đó, nó sẽ đi theo hướng Bắc ....

• Bài 24 trang 89 SBT Toán 9 Tập 1: Từ một máy bay trực thăng, một người đặt mắt tại vị trí M ở độ cao MH = 920 m. Người đó nhìn hai vị trí A và B của ...

• Bài 25 trang 89 SBT Toán 9 Tập 1: Từ một đài quan sát, một người đặt mắt tại vị trí B. Người đó nhìn thấy một chiếc ô tô ở vị trí C theo phương BC tạo với phương nằm ngang Bx ....

• Bài 26 trang 89 SBT Toán 9 Tập 1: Flycam là từ viết tắt của Fly camera. Đây là thiết bị bay không người lái có lắp camera hay máy ảnh để quay phim hoặc chụp ảnh từ trên cao....