Cho tam giác ABE vuông cân tại A với AB = AE = 2a, Vẽ đường tròn tâm O đường kính AB

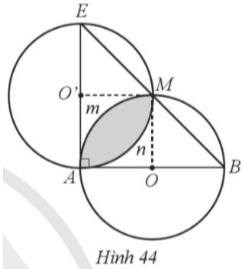
Cho tam giác ABE vuông cân tại A với AB = AE = 2a. Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O’ đường kính AE. Gọi M là giao điểm khác A của hai đường tròn (O), (O’) (Hình 44).

Giải SBT Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên - Cánh diều

Bài 40 trang 121 SBT Toán 9 Tập 1: Cho tam giác ABE vuông cân tại A với AB = AE = 2a. Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O’ đường kính AE. Gọi M là giao điểm khác A của hai đường tròn (O), (O’) (Hình 44).

Tính theo a:

a) Độ dài cung AmM và cung AnM tương ứng của đường tròn (O) và (O’);

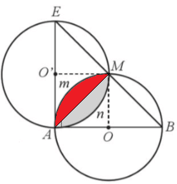
b) Diện tích của phần tô màu xám theo a.

Lời giải:

a) Ta có O, O’ lần lượt là trung điểm của AB, AE, mà AB = AE nên AO = AO’ = a.

Mà M là giao điểm của (O) và (O’) nên OM = OA và O’M = O’A.

Do đó OA = OM = O’A = O’M  = a, nên AOMO’ là hình thoi

Lại có $\widehat{OA{O}^{\text{'}}}=90°$ nên AOMO’ là hình vuông. Suy ra $\widehat{AOM}=\widehat{A{O}^{\text{'}}M}=90°.$

Do đó, độ dài cung AmM và cung AnM tương ứng của đường tròn (O) và (O’) cùng bằng $\frac{\pi a\cdot 90}{180}=\frac{\pi a}{2}.$

Nối A với M. Khi đó diện tích của phần tô màu xám bằng 2 lần diện tích phần tô màu đỏ tạo bởi dây AM và cung AmM của đường tròn (O), và bằng 2 lần hiệu diện tích của hình quạt tròn bán kính a, cung có số đo 90° và diện tích tam giác OAM.

Diện tích của hình quạt tròn bán kính a, cung có số đo 90° là:

$\frac{\pi a^2\cdot 90}{360}=\frac{\pi a^2}{4}$ (đơn vị diện tích).

Diện tích của tam giác OAM là: $\frac{1}{2}OA\cdot OM=\frac{a^2}{2}$ (đơn vị diện tích).

Diện tích của phần tô màu đỏ là: $\frac{\pi a^2}{4}-\frac{a^2}{2}=\frac{\left(\pi -2\right)a^2}{4}$ (đơn vị diện tích).

Vậy diện tích của phần tô màu xám là:

$2\cdot \frac{\left(\pi -2\right)a^2}{4}=\frac{\left(\pi -2\right)a^2}{2}$ (đơn vị diện tích).

Lời giải SBT Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên hay khác:

• Bài 37 trang 120 SBT Toán 9 Tập 1: Hoàn thành số liệu ở bảng sau (làm tròn kết quả đến hàng phần trăm của đơn vị đo đã cho nếu cần, lấy π ≈ 3,14): ....

• Bài 38 trang 120 SBT Toán 9 Tập 1: Chuyển động của Mặt Trăng quanh Trái Đất theo một quỹ đạo là gần giống đường tròn với tốc độ không đổi. Giả thiết quỹ đạo này là đường tròn ....

• Bài 39 trang 121 SBT Toán 9 Tập 1: Cho hình thoi ABCD có cạnh AB = 5 cm, đường chéo AC = 8 cm. Vẽ các đường tròn (A; 5 cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F ....

• Bài 41 trang 121 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R) ....

• Bài 42 trang 121 SBT Toán 9 Tập 1: Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A ....

• Bài 43 trang 122 SBT Toán 9 Tập 1: Cho hình chữ nhật ABCD với AB = 10 cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q ....

• Bài 44 trang 122 SBT Toán 9 Tập 1: Bác Long dự định mua gỗ để làm một mặt bàn. Mặt bàn có dạng ở giữa là hình chữ nhật với chiều rộng 1,2 m, chiều dài 1,8 m ....

• Bài 45 trang 122 SBT Toán 9 Tập 1: Hình 49 mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn (O; 15 cm), (O; 10 cm) ....

• Bài 46 trang 122 SBT Toán 9 Tập 1: Cho đường tròn tâm O bán kính OM = 8 cm. Gọi O’ là trung điểm của đoạn thẳng OM, vẽ đường tròn tâm O’ bán kính 16 cm. Trong đường tròn (O), kẻ dây AB đi qua O’ ....