Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ

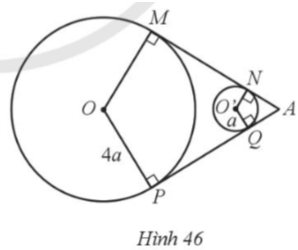
Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A sao cho (Hình 46). Tìm độ dài của dây Curoa mắc qua hai ròng rọc theo a.

Giải SBT Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên - Cánh diều

Bài 42 trang 121 SBT Toán 9 Tập 1: Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A sao cho $\widehat{MAP}=60°$ (Hình 46). Tìm độ dài của dây Curoa mắc qua hai ròng rọc theo a.

Lời giải:

Xét tứ giác ANO’Q có: $\widehat{AN{O}^{\text{'}}}+\widehat{AQ{O}^{\text{'}}}+\widehat{N{O}^{\text{'}}Q}+\widehat{NAQ}=360°$

Suy ra $\widehat{N{O}^{\text{'}}Q}=360°-\widehat{AN{O}^{\text{'}}}-\widehat{AQ{O}^{\text{'}}}-\widehat{NAQ}=360°-90°-90°-60°=120°.$

Tương tự, trong tứ giác AMOP ta cũng có $\widehat{MOP}=120°.$

Khi đó số đo của cung nhỏ NQ trong (O’) bằng 120° và số đo của cung lớn MP trong (O) bằng 360° – 120° = 240°.

Độ dài cung nhỏ NQ là: $l_1=\frac{\pi a\cdot 120}{180}=\frac{2\pi a}{3}.$

Độ dài cung lớn MP là: $l_2=\frac{\pi \cdot 4a\cdot 240}{180}=\frac{16\pi a}{3}.$

Do AM, AP là hai tiếp tuyến của (O) nên AM = AP và AO là tia phân giác của MAP.

Nên $\widehat{OAM}=\frac{1}{2}\widehat{MAP}=\frac{1}{2}\cdot 60°=30°.$

Xét ∆OAM vuông tại M có $AM=OM\cdot \cot \widehat{OAM}.$

Do AN, AQ là hai tiếp tuyến của (O’) nên AN = AQ và AO’ là tia phân giác của MAP.

Khi đó AO và AO’ trùng nhau.

Xét ∆O’AN vuông tại N có $AN=O^{\text{'}}N\cdot \cot \widehat{O^{\text{'}}AN}=O^{\text{'}}N\cdot \cot \widehat{OAM}.$

Ta có: $MN=PQ=AM-AN=OM\cdot \cot \widehat{OAM}-O^{\text{'}}N\cdot \cot \widehat{OAM}$

                 $=\left(OM-O^{\text{'}}N\right)\cdot \cot \widehat{OAM}=\left(4a-a\right)\cdot \cot 30°=3a\sqrt{3}.$

Độ dài của dây Curoa mắc qua hai ròng rọc là:

$\frac{2\pi a}{3}+\frac{16\pi a}{3}+2\cdot 3a\sqrt{3}=6a\left(\pi +\sqrt{3}\right).$

Lời giải SBT Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên hay khác:

• Bài 37 trang 120 SBT Toán 9 Tập 1: Hoàn thành số liệu ở bảng sau (làm tròn kết quả đến hàng phần trăm của đơn vị đo đã cho nếu cần, lấy π ≈ 3,14): ....

• Bài 38 trang 120 SBT Toán 9 Tập 1: Chuyển động của Mặt Trăng quanh Trái Đất theo một quỹ đạo là gần giống đường tròn với tốc độ không đổi. Giả thiết quỹ đạo này là đường tròn ....

• Bài 39 trang 121 SBT Toán 9 Tập 1: Cho hình thoi ABCD có cạnh AB = 5 cm, đường chéo AC = 8 cm. Vẽ các đường tròn (A; 5 cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F ....

• Bài 40 trang 121 SBT Toán 9 Tập 1: Cho tam giác ABE vuông cân tại A với AB = AE = 2a. Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O’ đường kính AE. Gọi M là giao điểm khác A ....

• Bài 41 trang 121 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R) ....

• Bài 43 trang 122 SBT Toán 9 Tập 1: Cho hình chữ nhật ABCD với AB = 10 cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q ....

• Bài 44 trang 122 SBT Toán 9 Tập 1: Bác Long dự định mua gỗ để làm một mặt bàn. Mặt bàn có dạng ở giữa là hình chữ nhật với chiều rộng 1,2 m, chiều dài 1,8 m ....

• Bài 45 trang 122 SBT Toán 9 Tập 1: Hình 49 mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn (O; 15 cm), (O; 10 cm) ....

• Bài 46 trang 122 SBT Toán 9 Tập 1: Cho đường tròn tâm O bán kính OM = 8 cm. Gọi O’ là trung điểm của đoạn thẳng OM, vẽ đường tròn tâm O’ bán kính 16 cm. Trong đường tròn (O), kẻ dây AB đi qua O’ ....